TimeWarp Editor
Extension of TimeWarp
Originally published • Last updatedDiscover how TimeWarp can be adapted to variably time scale one or more portions of a video.
TimeWarpEditor
The TimeWarp method for variably speeding up or slowing down video over the whole timeline is generalized to any number of editable subintervals of time.
Component Functions
The TimeWarp project generalized the Scaling Video Files project from constant time scaling to variable time scaling over the whole video timeline by introducing time scale functions. But it is sometimes desirable to speed up or slow down only portions of the video. This project generalizes TimeWarp for variably scaling video on any collection of subintervals of the whole video timeline.
TimeWarpEditor extends the method of TimeWarp so that different time scaling can be applied to any number of subintervals of the whole timeline, by associating each time scale function with a range. Use the new ComponentsEditor for defining a series of different time scaling functions on a collection of disjoint ranges of the whole timeline. These range based time scale functions are referred to as component functions, with a new struct named ComponentFunction.
The TimeWarp and Scaling Video Files discussions delve into the AVFoundation, vDSP and Quadrature (numerical integration) techniques shared by this project.
Time Scaling As Integration
TimeWarp implements a method that variably scales video and audio in the time domain. This means that the time intervals between video and audio samples are variably scaled along the timeline of the video according to time scaling factors that are functions of time. That contrasts with ScaleVideo in which the video was uniformly scaled by a single scaling factor.
In TimeWarp the instantaneous scaling function was defined:
Variable time scaling is interpreted as a function on the unit interval [0,1], called a unit function, that specifies the instantaneous time scale factor at each time in the video, with video time mapped to the unit interval with division by its duration D. It will be referred to as the instantaneous time scale function. The values v of the instantaneous time scale function will contract or expand infinitesimal time intervals dt variably across the duration of the video as v * dt.
In this way the absolute time scale factor at any particular time t is the sum of all infinitesimal time scaling up to that time, or the definite integral of the instantaneous scaling function from 0 to t/D, where D is the duration of the video. A corollary of that is the duration of the scaled video is the original duration D times the integral of the instantaneous time scaling function over the whole unit interval [0,1]. That’s how the estimated time of the scaled video is displayed in the user interface.
This idea is extended in TimeWarpEditor where time scaling is now performed as piecewise integration of a series of component functions, each defined on its own range in the video timeline.
Refer to the mathematical justification in TimeWarp for more discussion on how time scaling as integration works. Numerical integration, or Quadrature, is used to calculate the integrals of the built-in time scale functions.
Caveat: For technical reasons a scaling function s(t) = ∫ v(t) dt, the integral of an instantaneous scaling function v(t), must keep time ordered properly: it should not reverse the order of time. If two times ta and tb are ordered as:
ta < tb
Then it must be true that their scaled times are ordered the same:
ta * s(ta) < tb * s(tb)
One way to ensure that is for v(t) to always be positive so that s(t) = ∫ v(t) dt is always increasing.
TimeWarp Review: One Component Function
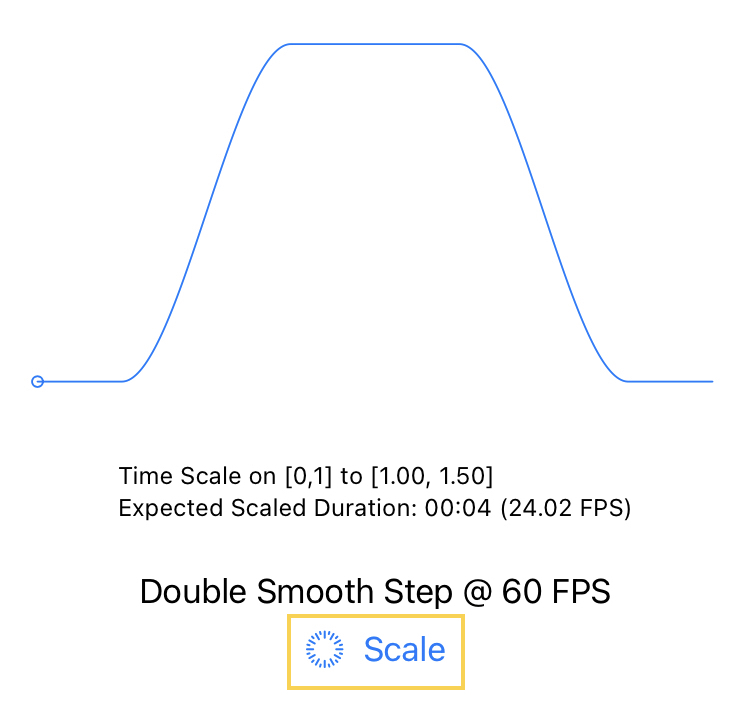
TimeWarp scales with a single instantaneous time scaling function, i.e. a single component function whose range is the whole video timeline.
The main view of TimeWarp displays a plot of the selected instantaneous time scaling function, chosen from a menu of built-in time scale functions.
Six sample time scale function types are defined in the TimeWarp project, named double smoothstep, power, tapered cosine, cosine, triangle and constant, with the following characteristic forms, respectively:
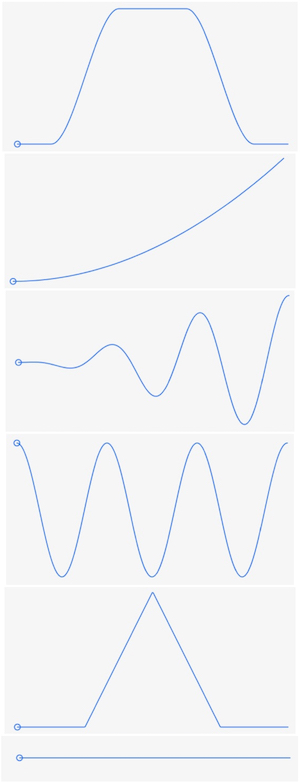
The built-in time scale functions are defined in a file UnitFunctions.swift along with other mathematical functions for plotting and integration.
The time scale functions have two associated parameters called factor and modifier that have different effects on each type, such as changing the magnitude, direction, frequency and rate of scaling. After specifying values for factor and modifier tap the scale button to apply the time scale function to the video and its audio, performed by the ScaleVideo class of TimeWarp on both the video frames and audio samples simultaneously.
TimeWarpEditor: Multiple Component Functions
In TimeWarpEditor one or more time scaling functions can be defined on disjoint subintervals of the whole timeline, using the new ComponentsEditor. Each subinterval is a ClosedRange contained in the unit interval [0,1]. These time scale functions are referred to as component functions.
To manage multiple component functions a new type has been defined, a struct named ComponentFunction, with a range field for specifying the subinterval of the unit interval over which it is defined.
struct ComponentFunction: Codable, Identifiable, CustomStringConvertible {
var range:ClosedRange<Double> = 0.0...1.0
var factor:Double = 1.5 // 0.1 to kComponentFactorMax
var modifier:Double = 0.5 // 0.1 to 1
var timeWarpFunctionType:TimeWarpFunctionType = .doubleSmoothstep
var id = UUID()
init() {
}
init(range:ClosedRange<Double>) {
self.range = range
}
init?(range:ClosedRange<Double>, factor:Double, modifier:Double, timeWarpFunctionType: TimeWarpFunctionType) {
guard range.lowerBound >= 0, range.lowerBound < 1.0, range.upperBound > 0, range.upperBound <= 1.0 else {
return nil
}
guard factor >= 0.1, factor <= kComponentFactorMax, modifier >= 0.1, modifier <= 1 else {
return nil
}
self.range = range
self.factor = factor
self.modifier = modifier
self.timeWarpFunctionType = timeWarpFunctionType
}
var description: String {
"\(range), \(factor), \(modifier), \(timeWarpFunctionType)"
}
}
Every ComponentFunction has a type TimeWarpFunctionType, extending the types in the TimeWarp project with some new built-in time scaling functions, like smoothstep, and a new option to flip any non-symmetrical time scaling function along the time domain. A flipped version m(t) of a unit function f(t) is defined as m(t) = f(1-t).
enum TimeWarpFunctionType: String, Codable, CaseIterable, Identifiable {
case doubleSmoothstep = "Double Smooth Step"
case smoothstep = "Smooth Step"
case smoothstepFlipped = "Smooth Step Flipped"
case triangle = "Triangle"
case cosine = "Cosine"
case cosineFlipped = "Cosine Flipped"
case sine = "Sine"
case sineFlipped = "Sine Flipped"
case taperedCosine = "Tapered Cosine"
case taperedCosineFlipped = "Tapered Cosine Flipped"
case taperedSine = "Tapered Sine"
case taperedSineFlipped = "Tapered Sine Flipped"
case constant = "Constant"
case power = "Power"
case power_flipped = "Power Flipped"
case constantCompliment = "Constant Compliment"
var id: Self { self }
}
Only non-symmetric types for which flipping makes sense, i.e. f(1-t) != f(t), have flipped types and TimeWarpFunctionType has some extensions to help with that:
extension TimeWarpFunctionType {
func flippedType() -> TimeWarpFunctionType? {
return TimeWarpFunctionType(rawValue: self.rawValue + " Flipped")
}
func unflippedType() -> TimeWarpFunctionType {
let rawValue = self.rawValue.replacingOccurrences(of: " Flipped", with: "")
return TimeWarpFunctionType(rawValue:rawValue) ?? .doubleSmoothstep
}
func isFlipped() -> Bool {
self.rawValue.hasSuffix(" Flipped")
}
static func allUnFlipped() -> [TimeWarpFunctionType] {
return TimeWarpFunctionType.allCases.filter { type in
type.isFlipped() == false
}
}
}
Component Validation
Component validation is the process of assuring the set of component functions make sense. The series of component functions will be applied cumulatively for time scaling, meaning that they will be piecewise integrated on [0,t] to calculate the scaling factor at a time t. Validation includes ensuring all ranges have non-zero length, do not overlap, are subintervals of unit interval [0,1] and are sorted in time.
Component validation also includes combining the user defined set of time scaling component functions with a set of time scaling functions that do not scale at all, but apply constant scaling with a scale factor of 1. These are named constant compliments since they are defined on the complimentary set of user defined components.
The function constantCompliments returns an array of ComponentFunction where each component function has type .constantCompliment, or nil if there are no compliments.
func constantCompliments(_ components:[ComponentFunction]) -> [ComponentFunction]?
The function addConstantCompliments will use constantCompliments to append the user defined component functions with constant compliments, perform other validation and sorting.
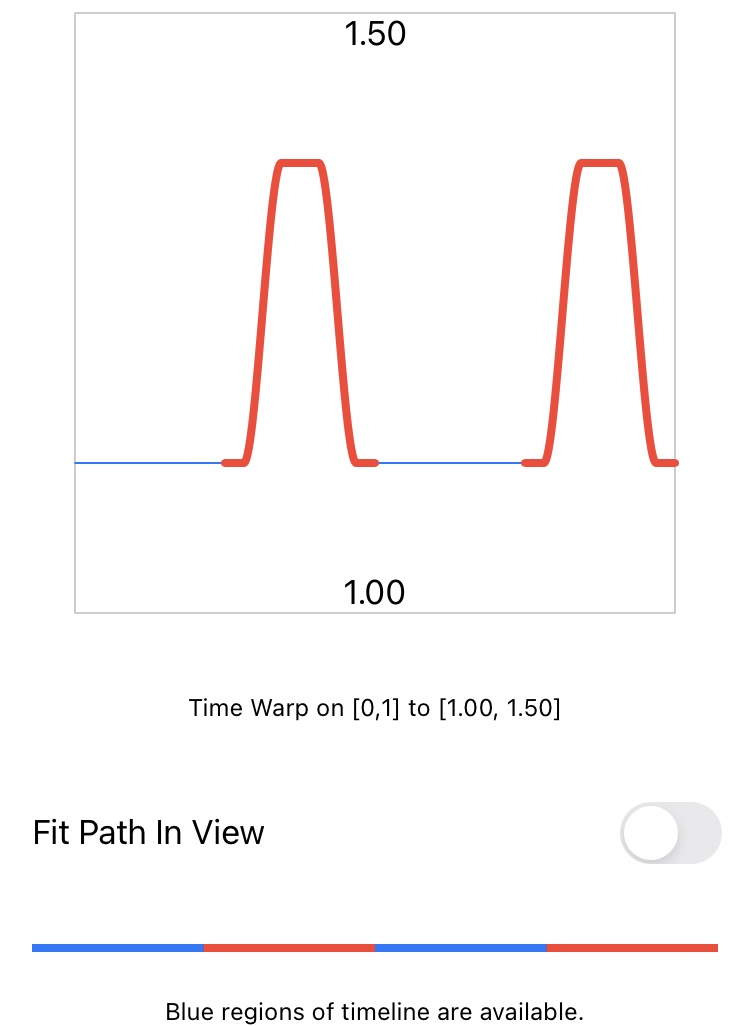
Components Editor
In the ComponentsEditor main view the user defined component functions are plotted alongside a red and blue timeline below, blue ranges of the constant compliments, and red ranges of user defined components.
The Edit button in the main view of this project opens the ComponentsEditor where a table of selected time scale functions is presented.
Each row of the table displays component function property values, and an edit button that opens up the ComponentEditor. Each component function row has a linear graphic illustrating its range, as red over blue, within the unit interval [0,1].
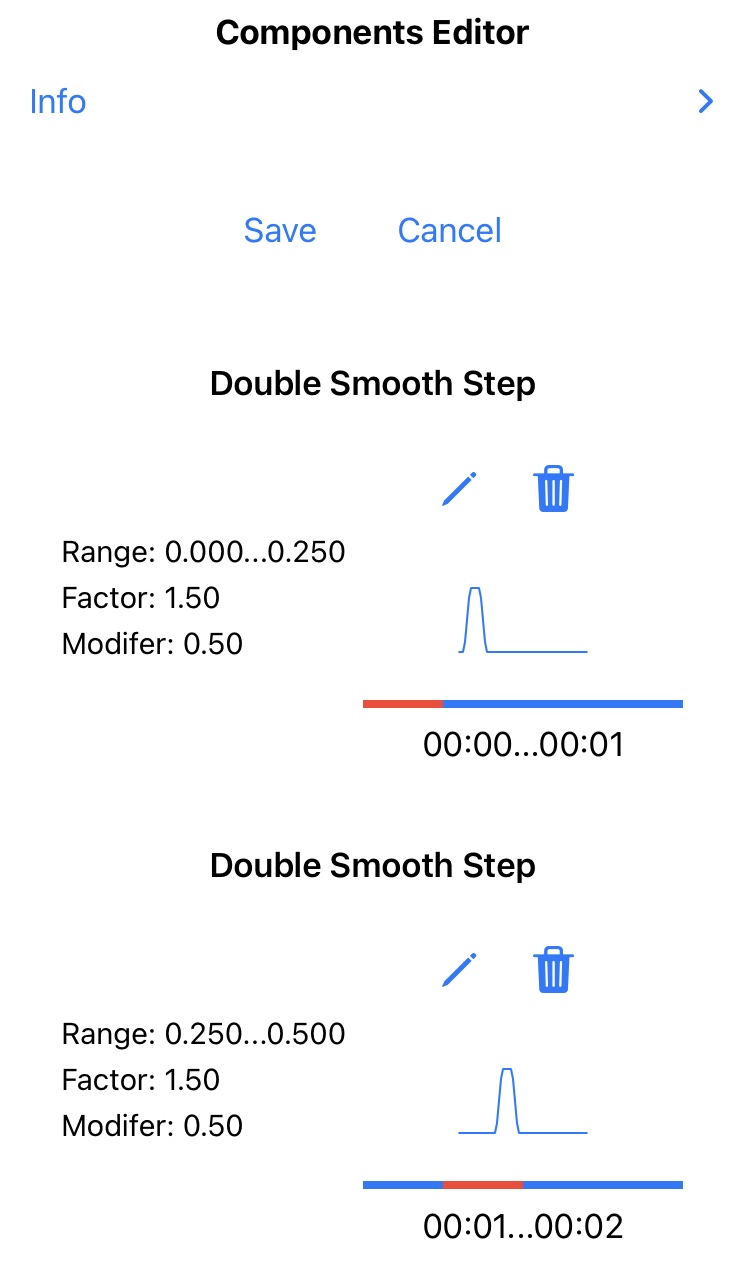
Below the table is plot of all the component functions, which also appears in the main view. A linear graphic illustrates all component ranges, as red over blue, within the unit interval [0,1]. Tap on the plot also to select and highlight specific components, with matching selection in the table.
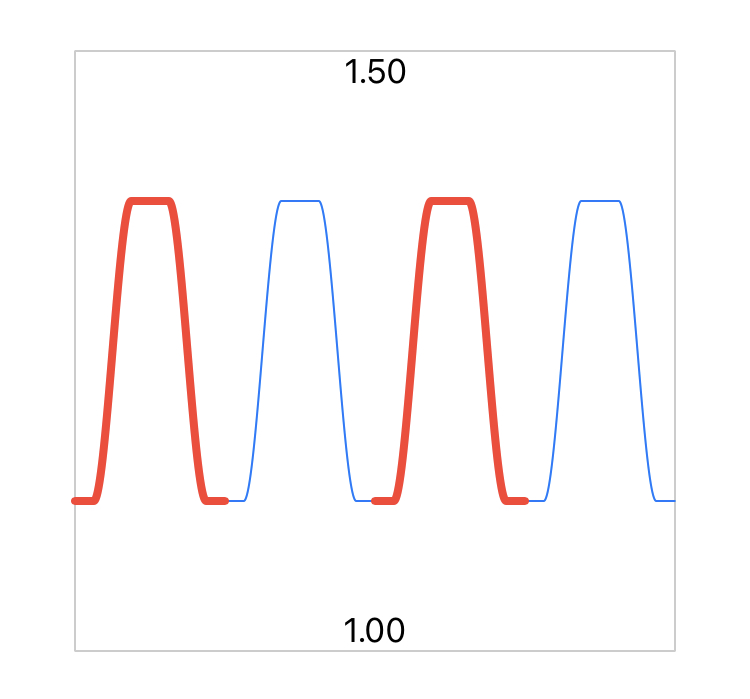
Each component function listed is configured in the ComponentEditor, just as it was in TimeWarp, but including one other specification, namely the time range of the video over which it applies.
A time range selector is provided for choosing the range.

Two video players and plot of the video audio serve to help select the desired video interval:
- The left player displays the frame of the video at time corresponding to the left end of the selected interval, and the right player displays the frame of the video at time corresponding to the right end of the selected interval.
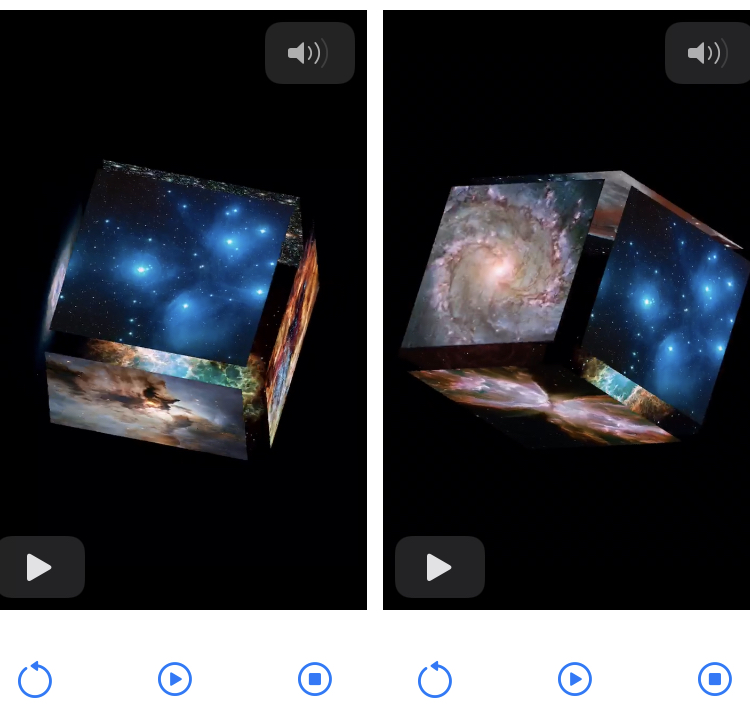
- A yellow frame overlay of the audio plot indicates the portion of the audio included in the selected interval.

Audio is plotted in an interactive waveform view with the classes discussed in the project PlotAudio.
Time scaling is performed by the TimeWarpVideoGenerator class of TimeWarpEditor on both the video frames and audio samples simultaneously. TimeWarpVideoGenerator is functionally identical to the class ScaleVideo in TimeWarp with name substitutions, such as TimeWarpVideoGenerator for ScaleVideo, and timeWarping for scaling.
Integration by Change Of Variables
During the process of piecewise integration of the series of component functions it will be necessary to evaluate the integral of each component function on its own range. This will be performed by the following component integration function:
func integrate(_ t:Double, componentFunction:ComponentFunction) -> Double?
Time scale functions f(t), as unit functions, are defined on the unit interval [0,1] and applied on other intervals [a,b] with a linear transformation h(t) between the intervals, h:[a,b]->[0,1].
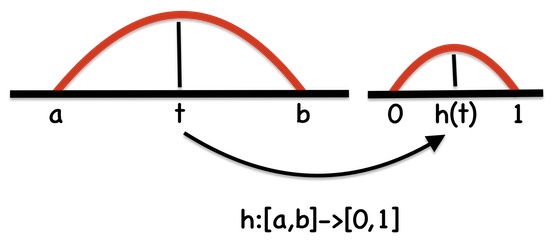
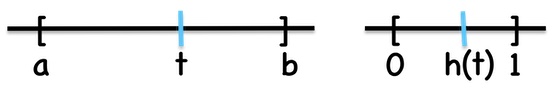
The integral of each component function over the subinterval of the video timeline on which it is defined is actually calculated as the integral over a subinterval of the unit interval. The Change of Variables formula is applied to evaluate integrals in unit interval domain.
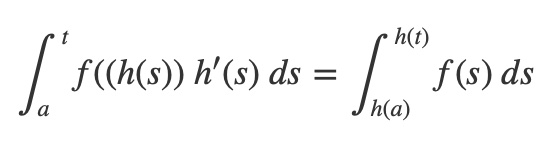
The change of variables linear mapping h(t) is suggested by the following diagram,
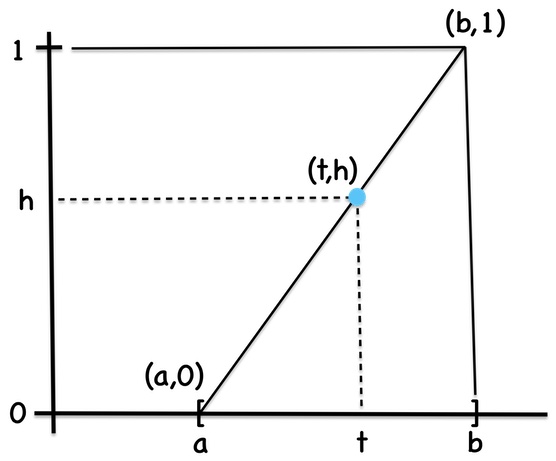
Given by:
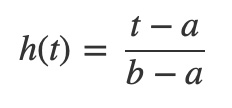
The derivative h'(t) is:
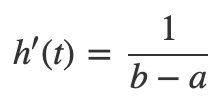
Substituting h(t) and h'(t) in the change of variables formula yields an expression for the integral of the time scaling function over the subinterval [a,t] of the range [a,b] as an integral in the unit interval over [0,(t-a)/(b-a)]:
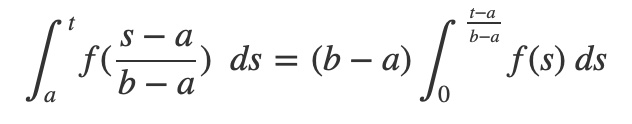
This relation is used in the implementation of the following component integration function, used in the process of time scaling a series of component functions, by individually integrating each component function and summing the results:
func integrate(_ t:Double, componentFunction:ComponentFunction) -> Double?
Note that component functions ranges are subintervals of the unit interval [0,1]. Therefore in the discussion above, if [a,b] is the range of a component function then it is contained in the unit interval [0,1], as for example here:

Time Scaling Implementation
Time scaling as integration of a series of component functions, each defined on a subinterval of the whole timeline, is implemented as piecewise integration in UnitFunctions.swift in the method integrateComponents.
This section discusses the various functions that take part in the process, listed below in the order invoked:
// TimeWarpVideoObservable.swift
func warp() {...} // start scaling video and audio
func integrator(_ t:Double) -> Double {...} // integrates scaling function
// TimeWarpVideoGenerator.swift
func timeScale(_ t:Double) -> Double? {...} // compute scale factor with integrator
// UnitFunctions.swift
func integrateComponents(_ t:Double, components:[ComponentFunction]) -> Double? {...} // iterate component functions
func integrate(_ t:Double, componentFunction:ComponentFunction) -> Double? {...} // prepare integration for current component
func integrator(for componentFunction:ComponentFunction) -> (Double,Double,Double)->Double? {...} // lookup specific integration function for current component
func quadrature_integrate(_ t:Double, integrand:(Double)->Double) -> Double? {...} // perform numerical integration
Time Scaling Video Frames
Go to Time Scaling Implementation
Consider how the presentation time of a video frame in the scaled video is computed. The function writeVideoOnQueueScaled retrieves the video frame presentation time as seconds and scales it with timeScale:
var presentationTimeStamp = CMSampleBufferGetPresentationTimeStamp(sampleBuffer)
let timeToScale:Double = presentationTimeStamp.seconds
if let presentationTimeStampScaled = self.timeScale(timeToScale) {
...
}
The method timeScale performs the integration of the time scaling function:
func timeScale(_ t:Double) -> Double?
{
var resultValue:Double?
resultValue = integrator(t/videoDuration)
if let r = resultValue {
resultValue = r * videoDuration
}
return resultValue
}
The method timeScale employs the change of variables formula for integration:
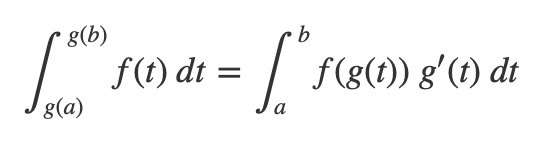
The change of variables mapping g from video time to unit interval time is a linear mapping that scales time with division by the video duration D:
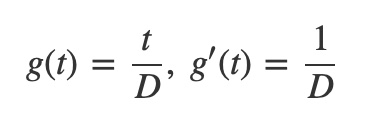
Substitute into the change of variables formula to obtain:
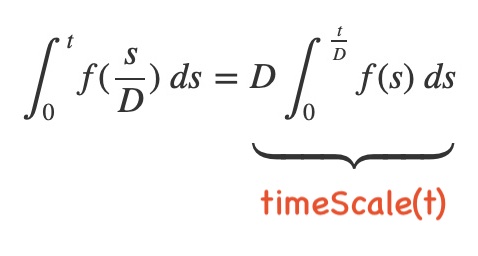
The timeScale method is implementing the right hand side of this formula, where the integrator is the integral of the time scaling function in the unit interval domain.
The integrator is a property of TimeWarpVideoGenerator:
var integrator: ((Double) -> Double)
It is passed to the init method, and the videoDuration is computed in the init:
self.videoDuration = self.videoAsset.duration.seconds
The TimeWarpVideoGenerator is instantiated in the warp() method of the TimeWarpVideoObservable, with the integrator passed as an argument, and started:
self?.timeWarpVideoGenerator = TimeWarpVideoGenerator(path: path, frameRate: Int32(fps), destination: destinationPath, integrator: integrator, progress: {
...
}, completion: {
...
})
self?.timeWarpVideoGenerator?.start()
The method warp() is invoked by the Time Warp button in the user interface:
Button(action: { timeWarpVideoObservable.warp() }, label: {
Label("Time Warp", systemImage: "timelapse")
})
The integrator is what differentiates time scaling in TimeWarpEditor from TimeWarp. It is a method of TimeWarpVideoObservable that calls the Unit Functions.swift method integrateComponents, which performs the piecewise integration of a series of component functions, validatedComponentFunctions:
func integrator(_ t:Double) -> Double {
return integrateComponents(t, components: self.validatedComponentFunctions) ?? 1
}
In TimeWarp the integrator only integrated one time scaling function, making it much simpler. See ScaleVideoObservable.
The validatedComponentFunctions is a published array of ComponentFunction:
@Published var validatedComponentFunctions = [ComponentFunction()]
The user interface provides the ability to construct a valid array of component functions, namely the ComponentsEditor, as described in TimeWarpEditor: Multiple Component Functions.
Validation ensures the sequence of component functions are ordered in time, so that the upper bound of each component range is less than or equal to the lower bound of any successive component range. This is important for the piecewise integration in integrateComponents, discussed next.
Unit Functions Integration
Go to Time Scaling Implementation
Integration is ultimately performed with numerical integration using Quadrature during the piecewise integration of component functions, starting with integrateComponents:
- Iterate Components - iterate components and integrate each component whose range overlaps the range of the time scaling integral
- Lookup Integrators - find the integrators for integrating the current component type
TimeWarpFunctionTypein the iteration - Component Integration Function - the component integration function invokes the integrator using change of variables
- Numerically Integrate - the integrator performs numerical integration using quadrature
Iterate Components
Go to Unit Functions Integration
Given a unit interval time t, mapped from video time by division with the video duration D, the function integrateComponents performs piecewise integration of the components in the argument components array on the subinterval [0,t] of unit interval [0,1].
integrateComponents calls the component integration function integrate to integrate component functions within their ranges.
func integrateComponents(_ t:Double, components:[ComponentFunction]) -> Double? {
var value:Double = 0
for component in components {
if contains(t, componentFunction: component) {
// integrate up to t in component range
if let integral = integrate(t, componentFunction: component) {
value += integral
return value
}
}
// integrate over whole component range
if let integral = integrate(component.range.upperBound, componentFunction: component) {
value += integral
}
}
return value
}
Although integrateComponents does not check, it is assumed that the array of components have been sorted by time, a requirement of component validation. integrateComponents iterates the array of time sorted components, and for each component determines if its range contains the time t:
If the range does not contain t the whole integral for that component is added to the running total value. Otherwise the integral of the component containing t is integrated up to time t, updates and returns the running total, ending piecewise integration.
Lookup Integrator
Go to Unit Functions Integration
The integrator is the function that actually performs integration of a component function. Every component has its own integrator, just as each has its own graphical plotting method.
The component integration function integrate(t:componentFunction:) called by integrateComponents invokes the lookup method integrator(for:) associating the componentFunction with an integrator, the function for integrating that specific component type TimeWarpFunctionType:
func integrator(for componentFunction:ComponentFunction) -> (Double,Double,Double)->Double? {
switch componentFunction.timeWarpFunctionType {
case .doubleSmoothstep:
return integrate_double_smoothstep(_:factor:modifier:)
case .smoothstep:
return integrate_smoothstep(_:factor:modifier:)
case .smoothstepFlipped:
return integrate_smoothstep_flipped(_:factor:modifier:)
case .triangle:
return integrate_triangle(_:factor:modifier:)
case .cosine:
return integrate_cosine(_:factor:modifier:)
case .cosineFlipped:
return integrate_cosine_flipped(_:factor:modifier:)
case .sine:
return integrate_sine(_:factor:modifier:)
case .sineFlipped:
return integrate_sine_flipped(_:factor:modifier:)
case .taperedCosine:
return integrate_tapered_cosine(_:factor:modifier:)
case .taperedCosineFlipped:
return integrate_tapered_cosine_flipped(_:factor:modifier:)
case .taperedSine:
return integrate_tapered_sine(_:factor:modifier:)
case .taperedSineFlipped:
return integrate_tapered_sine_flipped(_:factor:modifier:)
case .constant:
return integrate_constant(_:factor:modifier:)
case .constantCompliment:
return integrate_constant(_:factor:modifier:)
case .power:
return integrate_power(_:factor:modifier:)
case .power_flipped:
return integrate_power_flipped(_:factor:modifier:)
}
}
For example, if the component has type .cosine then the integrator returned is integrate_cosine(_:factor:modifier:):
func integrate_cosine(_ t:Double, factor:Double, modifier:Double) -> Double? {
return quadrature_integrate(t, integrand: { t in
cosine(t, factor: factor, modifier: modifier)
})
}
The component integration function integrate(t:componentFunction:) discussed in the next section then invokes the integrator integrate_cosine to perform the numerical integration.
Component Integration Function
Go to Unit Functions Integration
The component integration function uses the integrator returned by integrator(for:) and the change of variables formula to integrate the component function in the unit time domain.
To apply the change of variables the time t must be mapped using unitmap, to set the upper bound of the integral:
func integrate(_ t:Double, componentFunction:ComponentFunction) -> Double? {
if let value = integrator(for:componentFunction)(unitmap(componentFunction.range.lowerBound, componentFunction.range.upperBound, t), componentFunction.factor, componentFunction.modifier) {
return value * (componentFunction.range.upperBound - componentFunction.range.lowerBound)
}
return nil
}
Where unitmap is defined as:
// map [x0,y0] to [0,1]
func unitmap(_ x0:Double, _ x1:Double, _ x:Double) -> Double {
return (x - x0)/(x1 - x0)
}
As per Integration by Change Of Variables, the value of the integral is multiplied by the length of the range of the component function, (componentFunction.range.upperBound - componentFunction.range.lowerBound):
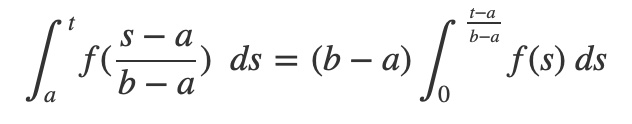
With unitmap mapping the component functions range to the unit interval as the change of variables:
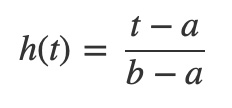
Numerically Integrate
Go to Unit Functions Integration
Finally, the integrators returned by integrator(for:) call quadrature_integrate where numerical integration is performed by the method Quadrature of Accelerate. There are two forms of quadrature_integrate, one for a scalar time t,
func quadrature_integrate(_ t:Double, integrand:(Double)->Double) -> Double?
And another for a range of time r:
func quadrature_integrate(_ r:ClosedRange<Double>, integrand:(Double)->Double) -> Double?
Both forms of quadrature_integrate take an integrand argument (Double)->Double) -> Double?, which is the function to be integrated.
let quadrature = Quadrature(integrator: Quadrature.Integrator.nonAdaptive, absoluteTolerance: 1.0e-8, relativeTolerance: 1.0e-2)
func quadrature_integrate(_ t:Double, integrand:(Double)->Double) -> Double? {
var resultValue:Double?
let result = quadrature.integrate(over: 0...t, integrand: { t in
integrand(t)
})
do {
try resultValue = result.get().integralResult
}
catch {
print("integrate error")
}
return resultValue
}
func quadrature_integrate(_ r:ClosedRange<Double>, integrand:(Double)->Double) -> Double? {
var resultValue:Double?
let result = quadrature.integrate(over: r, integrand: { t in
integrand(t)
})
do {
try resultValue = result.get().integralResult
}
catch {
print("integrate error")
}
return resultValue
}
Example 1 - Cosine
Some component integrators, like cosine, have a simple integrand.
For type .cosine the integrator is:
func integrate_cosine(_ t:Double, factor:Double, modifier:Double) -> Double? {
return quadrature_integrate(t, integrand: { t in
cosine(t, factor: factor, modifier: modifier)
})
}
And the cosine integrand is a single computation:
func cosine(_ t:Double, factor:Double, modifier:Double) -> Double {
factor * (cos(12 * modifier * .pi * t) + 1) + (factor / 2)
}
Example 2 - Triangle
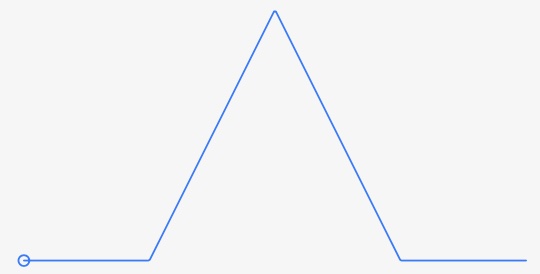
Other integrators, like triangle, are more complex.
The triangle, as a piecewise function of lines, involves multiple computations. The integrator is:
func integrate_triangle(_ t:Double, factor:Double, modifier:Double) -> Double? {
let c = 1/2.0
let w = c * modifier
return integrate_triangle(t, from: 1, to: factor, range: c-w...c+w)
}
Where integrate_triangle performs piecewise integration, similar to the form of integrateComponents.
func integrate_triangle(_ t:Double, from:Double = 1, to:Double = 2, range:ClosedRange<Double> = 0.2...0.8) -> Double? {
guard from > 0, to > 0, range.lowerBound >= 0, range.upperBound <= 1 else {
return 0
}
var value:Double?
let center = (range.lowerBound + range.upperBound) / 2.0
let r1 = 0...range.lowerBound
let r2 = range.lowerBound...center
let r3 = center...range.upperBound
let r4 = range.upperBound...1.0
guard let value1 = quadrature_integrate(r1, integrand: { t in
constant(from)
}) else {
return nil
}
guard let value2 = quadrature_integrate(r2, integrand: { t in
line(range.lowerBound, from, center, to, x: t)
}) else {
return nil
}
guard let value3 = quadrature_integrate(r3, integrand: { t in
line(range.upperBound, from, center, to, x: t)
}) else {
return nil
}
if r1.contains(t) {
value = quadrature_integrate(r1.lowerBound...t, integrand: { t in
constant(from)
})
}
else if r2.contains(t) {
if let value2 = quadrature_integrate(r2.lowerBound...t, integrand: { t in
line(range.lowerBound, from, center, to, x: t)
}) {
value = value1 + value2
}
}
else if r3.contains(t) {
if let value3 = quadrature_integrate(r3.lowerBound...t, integrand: { t in
line(range.upperBound, from, center, to, x: t)
}) {
value = value1 + value2 + value3
}
}
else if r4.contains(t) {
if let value4 = quadrature_integrate(r4.lowerBound...t, integrand: { t in
constant(from)
}) {
value = value1 + value2 + value3 + value4
}
}
return value
}
