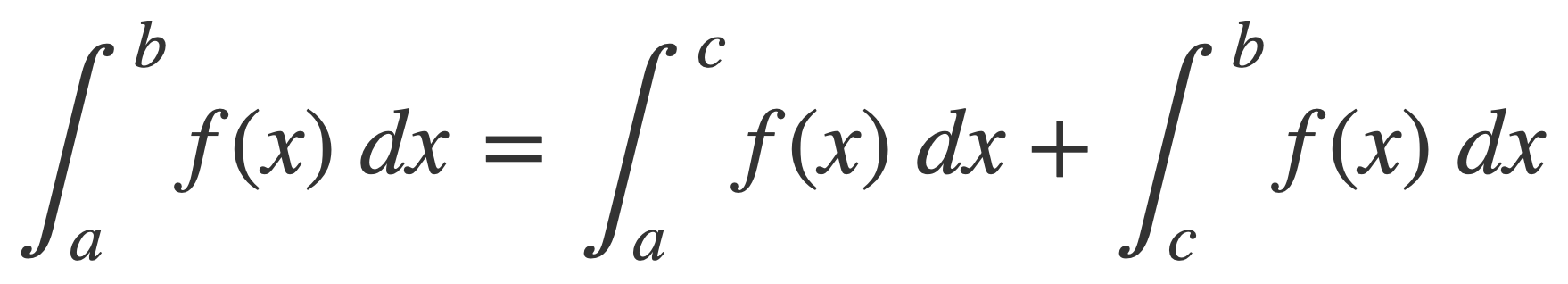ToneShaper
Create sounds graphically
Originally published • Last updatedAudio samples are generated with numerical integration of user defined instantaneous frequency curves.
ToneShaper
The associated Xcode project implements an iOS and macOS SwiftUI app that enables users to draw instantaneous frequency values to define a function of time, v(t). The function v(t) is numerically integrated with vDSP_vtrapzD to generate a time varying phase argument x(t) of a periodic function s(t). The composition s(x(t)) is sampled at a sufficient rate to produce audio samples of varying frequency for playing or writing to a file.
App Features
• The instantaneous frequency function v(t) is defined through two editing views, the plot view and the draw view.
• The width of each view corresponds to a selected time range [0, duration], while the height corresponds to a selected frequency range [minFrequency, maxFrequency].
• Users can tap within the plot view to select a series of points, subsequently subjected to linear interpolation by the vDSP.linearInterpolate function.
• Alternatively drag within the draw view: to select a series of points for transition to the plot view.
• Audio generation parameters are duration, frequency range, amplitude scaling, wave type, echo and fidelity, and are stored in documents. In-place document editing supports undo and redo. The samples library is a collection of built-in documents with parameter presets for starting points.
• Continuous audio play with AVAudioEngine provides feedback during experimentation with sound parameters before saving the sound as multiple cycles of the duration to a Linear PCM or MPEG-4 audio file.
Samples
ToneShaper Index
Prerequisite
Implementation
The prerequisite presents the terminology and concepts used to implement the variable tone generation, conveniently borrowed from TonePlayer. Sampling periodic functions at the proper rate and the use of instantaneous frequency during the sampling process will be needed for the implementation. The sections describing the implementation contain code samples that can be executed in an Xcode Swift Playground, and the source code to an app that generates this audio file:
Periodic Functions
A non-constant function f with the property f(t + c) = f(t) for a some constant c and all t is periodic, and the period is the smallest such c.
The sine and cosine functions are periodic by definition, as the coordinates on the unit circle determined by the angle θ:
Signals with period 1 are defined with the unit functions defined on the unit interval [0,1), extended to the whole real line using the decimal part of their argument. The decimal part of a number t is the remainder when dividing t by 1, mapping the number t into the unit interval [0,1), computed in Swift with the function truncatingRemainder:
let p = t.truncatingRemainder(dividingBy: 1)
For example:
var t = Double.pi
print("t = \(t)")
var p = t.truncatingRemainder(dividingBy: 1)
print("p = \(p)")
t = t + 1
print("t + 1 = \(t)")
p = t.truncatingRemainder(dividingBy: 1)
print("p = \(p)")
This logs:
t = 3.141592653589793 p = 0.14159265358979312 t + 1 = 4.141592653589793 p = 0.14159265358979312
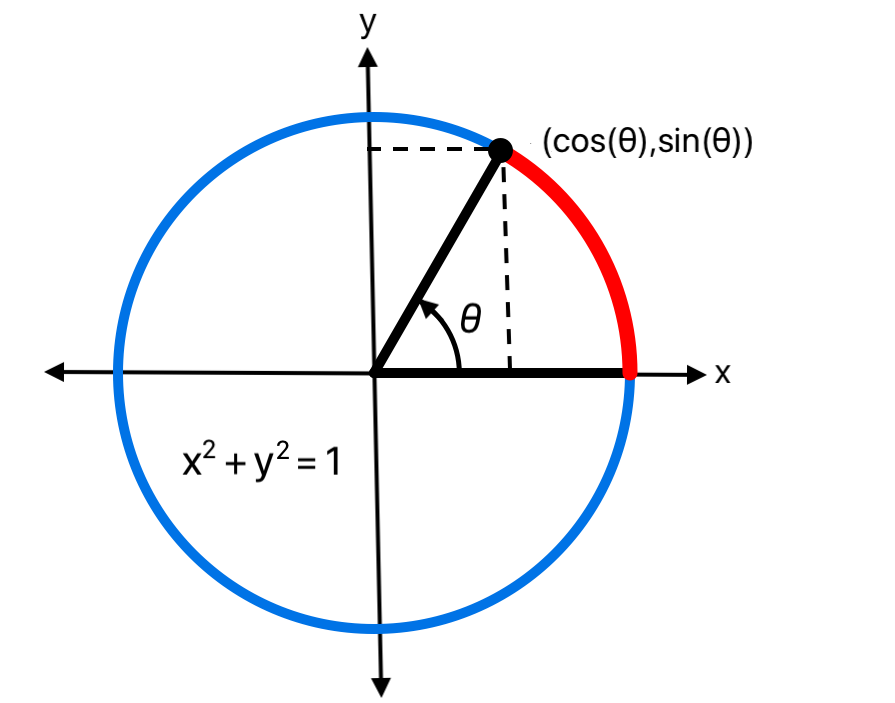
A unit function s(t) defined on [0,1) is evaluated for any t with s(t) = s(t.truncatingRemainder(dividingBy: 1), placing copies of the unit function along the real line. The unit function s(t) = sin(2 π t) is drawn this way here with two copies:
Angular vs. Oscillatory Frequency
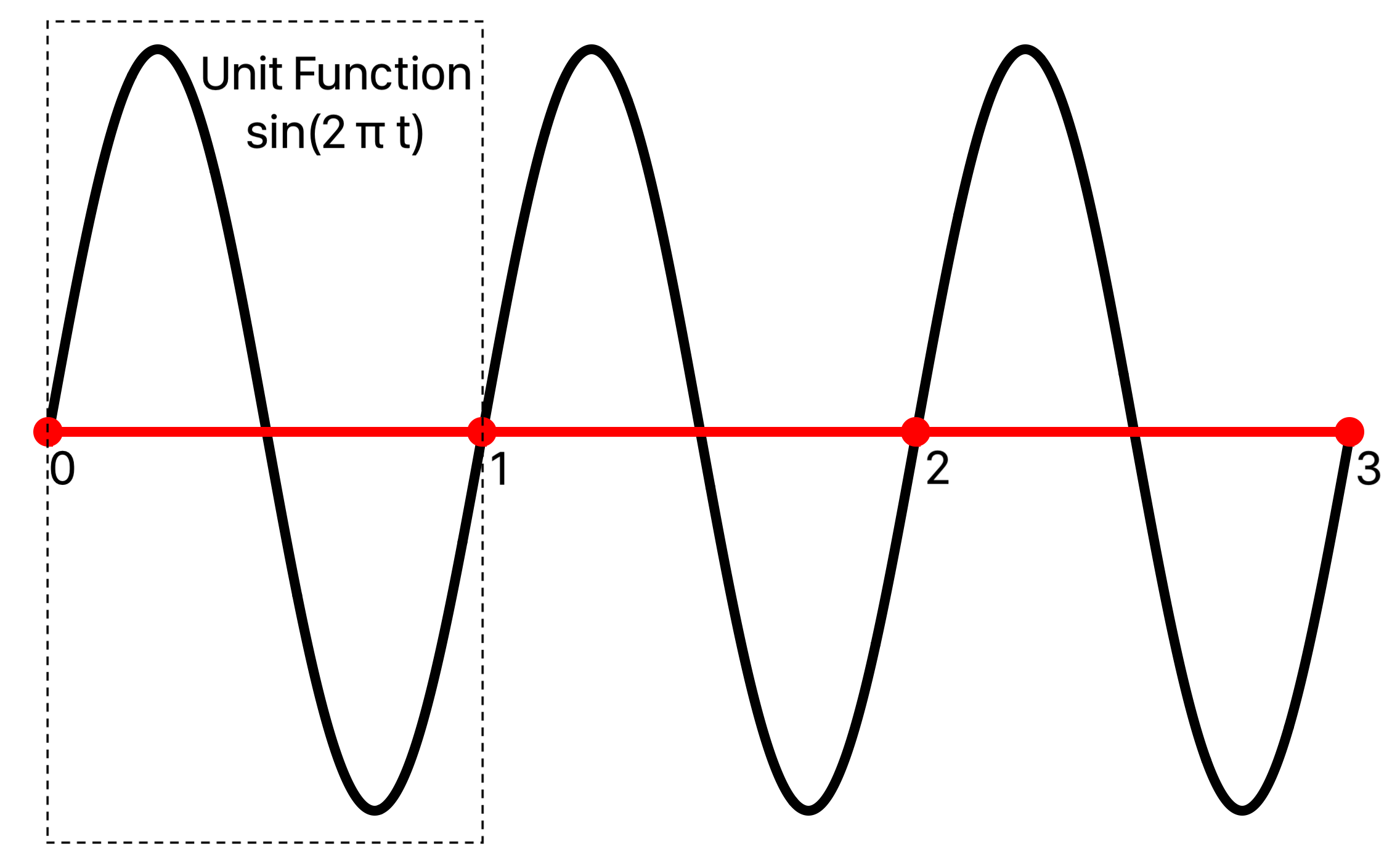
The measure θ of an angle is defined to be the arc length a it subtends on the unit circle, θ = a:
The unit of measure for angles is the radian, which is the angle that subtends an arc length of 1 on the unit circle, denoted by rad.
For a circle with radius r the total arc length C of its circumference is given by C = 2πr. Thus C = 2π for the unit circle, and a radian is the fraction 1/(2π) of its circumference C. A radian subtends the same fraction 1/(2π) of the circumference C of any other circle. But r = C/(2π), so a radian subtends an arc length r on a circle with radius r, hence the name radian.
Frequency is then defined in either oscillatory or angular units:
• Oscillatory frequency f is cycles per second, labelled hertz or Hz. For a periodic function with period k, oscillatory frequency f is f = 1/k, the number of periods in the unit interval [0,1].
• Angular frequency ω is the corresponding radians per second given by ω = 2πf, so 1 Hz (1 cycle per second) corresponds to 1 full angular revolution, or 2π radians per second.
The unit functions have oscillatory frequency of 1 Hz by definition. Signals with other oscillatory frequencies, or periods, are generated with the unit functions by scaling time.
Time Scaling Example
A unit function s(t) can be composed with a time varying function x(t) to obtain a new function s(x(t)) that has period k, for any k. This function is x(t) = t/k, for some constant k, then g(t) = s(x(t)) = s(t/k) is a function with period k, as seen here using the unit periodicity of s:
g(t + k) = s((t + k) / k) = s(t/k + 1) = s(t/k) = g(t).
For example, to generate a signal with 4 Hz, scale time by 4:
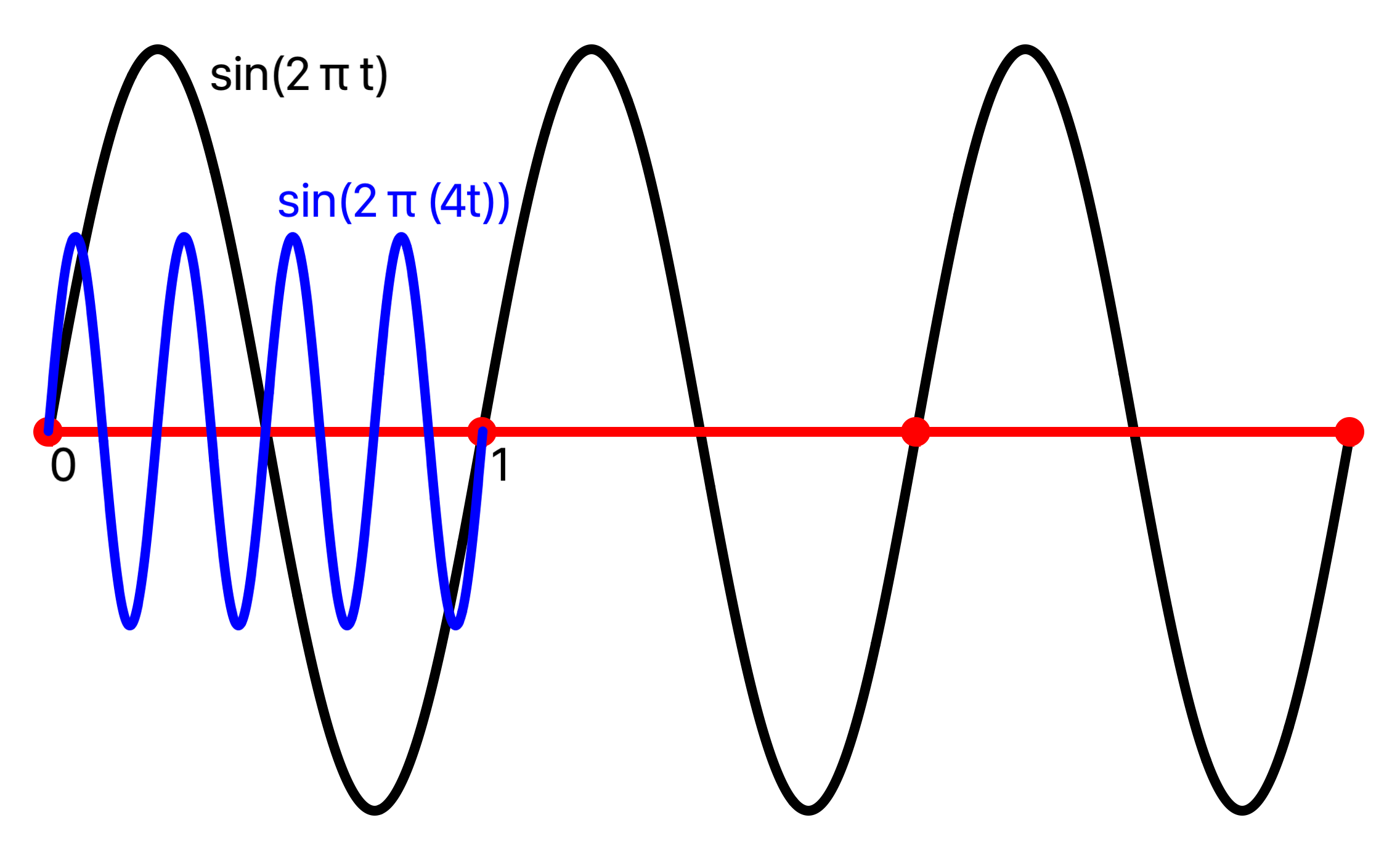
Tone Generation
In physics sound is the mechanical vibrations of air that can induce electric signals in devices such as a microphone. The voltage of the electric signal can then be quantized into amplitudes, by sampling over time with an analog-to-digital converter and stored as an array of sample values in a digital audio or video media file.
Sound can also be generated from samples using mathematical functions that model physical sources. An idealized pure tone can be modeled by sampling a periodic function s(t) and played using AVAudioEngine. This means that s(t) is evaluated on an indexed grid of enough incremental time intervals, with increments of size delta_t determined by the sampleRate, to fill an audio buffer of a size requested by AVAudioEngine in the AVAudioSourceNodeRenderBlock of the AVAudioSourceNode.
let delta_t:Double = 1.0 / Double(sampleRate)
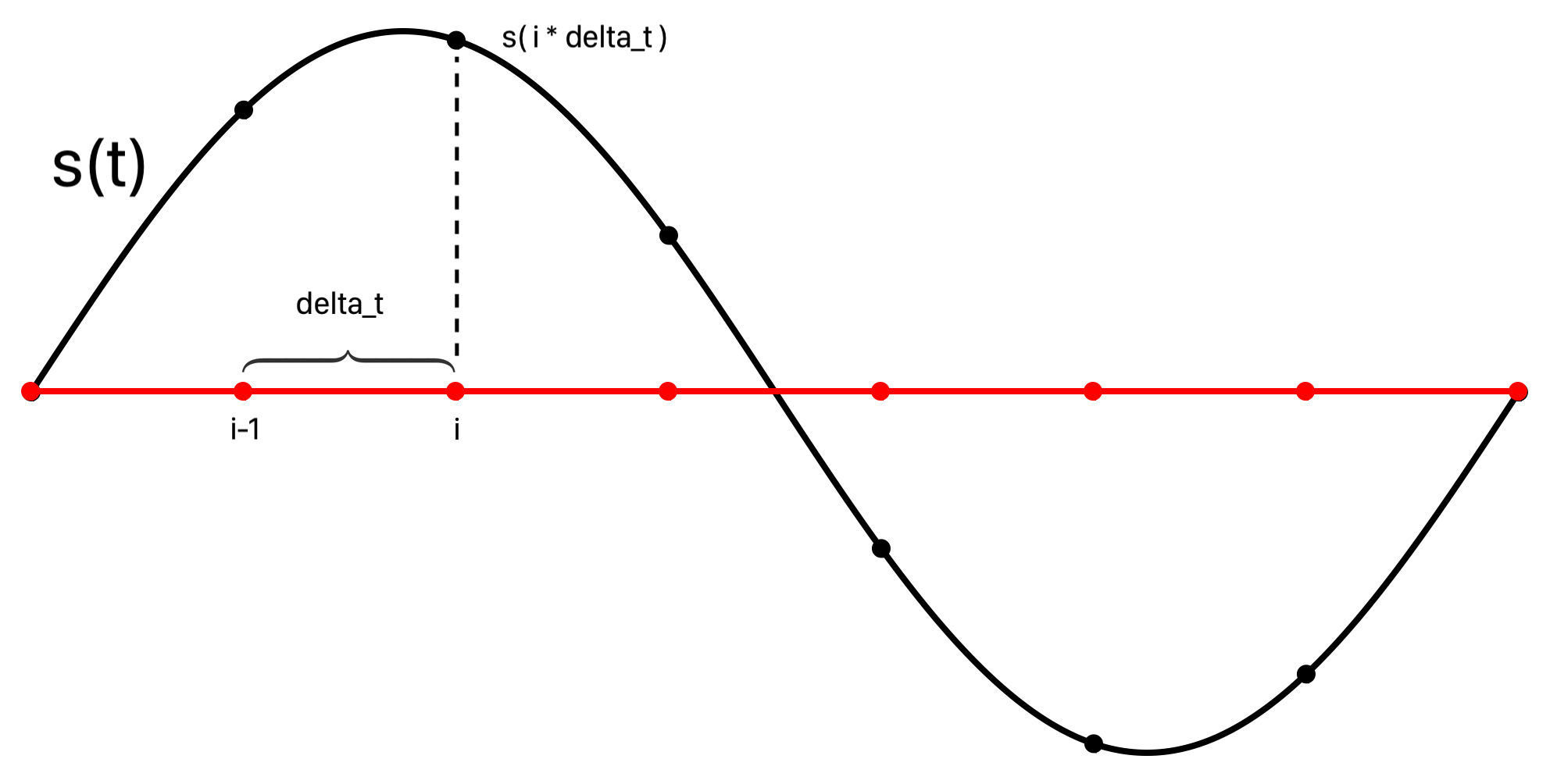
In this application the sample rate is provided by AVAudioEngine at the time it is set up:
let output = engine.outputNode
let outputFormat = output.inputFormat(forBus: 0)
sampleRate = Float(outputFormat.sampleRate)
print("The audio engine sample rate is \(sampleRate)")
This printed:
"The audio engine sample rate is 44100.0"
When AVAudioEngine is set up an AVAudioSourceNode named srcNode is created with an AVAudioSourceNodeRenderBlock, a function that is called repeatedly to request audio sample buffers for playing. In this block the number of samples requested named frameCount is provided, which along with the cumulative sample count named currentIndex determines the sampleRange, a range of indices ClosedRange<Int> for the grid’s array of samples.
let sampleRange = currentIndex...currentIndex+Int(frameCount-1)
The sample range sampleRange for the current audio buffer is passed to a function audioSamplesForRange where it is iterated to compute the sample times at which to evaluate signal s(t).
for i in sampleRange.lowerBound...sampleRange.upperBound {
let t = Double(i) * delta_t
// ... evaluate s(t)
}
audioSamplesForRange returns the samples as an array [Int16] that are then added as Float to the AudioBuffer provided by the AVAudioSourceNodeRenderBlock.
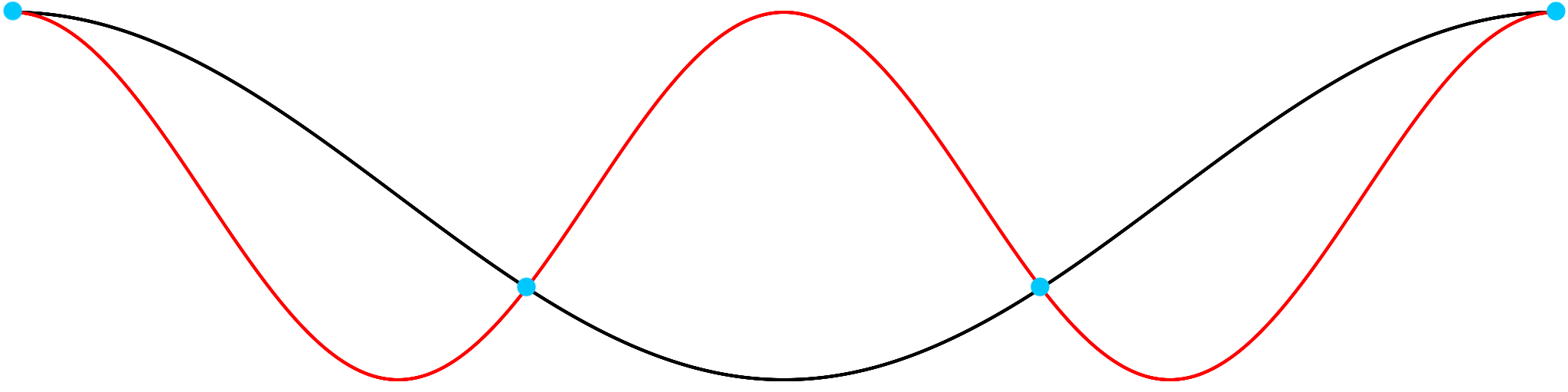
The high sample rate required for audio is due to the classical Nyquist-Shannon sampling theorem which says that a band-limited signal with maximum frequency B can be exactly reconstructed from samples if the sample rate R is twice the maximum frequency B, or R = 2B. Otherwise aliasing occurs, and the reconstructed signal misrepresents the original. Consequently for your hearing range up to 20,000 cycles per second (20kHz) a sample rate greater than 2 x 20,000 = 40,000 samples per second is required. In practice, the sample rate should be chosen strictly greater than twice the maximum frequency B, or R > 2B.
The Fourier transform determines the frequency components of a signal to find the maximum frequency B. If B does not exist, the signal has unlimited frequency components and aliasing occurs for any sample rate. Illustrated here is a higher frequency red signal, which always exists when there is no highest frequency, that is undersampled for a sample rate sufficient for the lower frequency black signal. The blue dot samples are the same for each but miss details of the red signal, causing the red signal to be aliased and indistinguishable from the black signal:
Instantaneous Frequency
Frequency can be time dependent, or variable, by composing a constant frequency signal s(t) of 1 Hz with a time scaling function x(t). The derivative v(t) = dx(t)/dt is the instantaneous rate of change of x(t), or instantaneous frequency. Also x(t) is given by integration of v, x(t) = ∫ v(t):
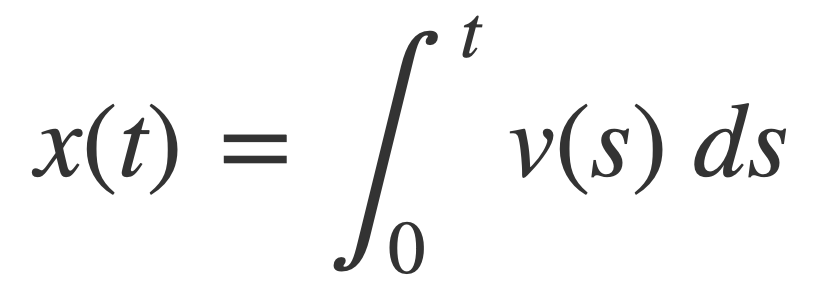
The antiderivative x(t) can be interpreted as a distance traversed at time t in units of the period 1 of s(t), and v(t) as the speed traversing those periods.
In this way a signal s(x(t)) with specific variable frequency can be created by defining v(t) appropriately. As AVAudioEngine requests sample buffers to play and the frequency slider changes, the argument x(t) for the current signal s(t) is updated for smooth play. This is achieved by defining the x(t) as the integral of an instantaneous frequency function v(t) that linearly interpolates the frequency values at the start and end times of the current sample buffer. This means that v(t) = dx/dt, the derivative of x(t), is a frequency ramp.
Previously, in the Time Scaling Example a signal g was defined as:
g(t) = s(x(t)) = s(t/k)
Let f = 1/k, and x(t) = f t, then the rate of change of x is the constant frequency f:
dx(t)/dt = f
and
g(t) = s(x(t)) = s(f t)
Conversely when the rate of change v is a constant f, then x(t) is a linear function f * t + p, for any constant p:
x(t) = ∫ v(t) = ∫ f = f * t + p
For example applying this to the unit function sin(2 π t) with p = 0, the substitution yields sin(2 π f t), the sine wave with constant frequency f Hz.
Constant vs Variable Frequency
The instantaneous rate of change v(t) = dx(t)/dt is illustrated for constant and variable speed to see how the resulting argument x(t) affects the waveform and remaps the periods of the unit function sin(2 π t) with period 1.
Two cases are considered:
1. Constant Instantaneous Frequency
In the case of constant speed 3, v(t) = 3, the periods of sin(2 π t) are traversed at the rate of 3 periods per second, or a constant frequency of 3. This is observed in the composed plot sin(2 π x(t)) = sin(2 π (3 t)) with uniformly spaced crests as time goes on.
The instantaneous frequency is v(t) = 3, with argument given by the antiderivative x(t) = 3 t:
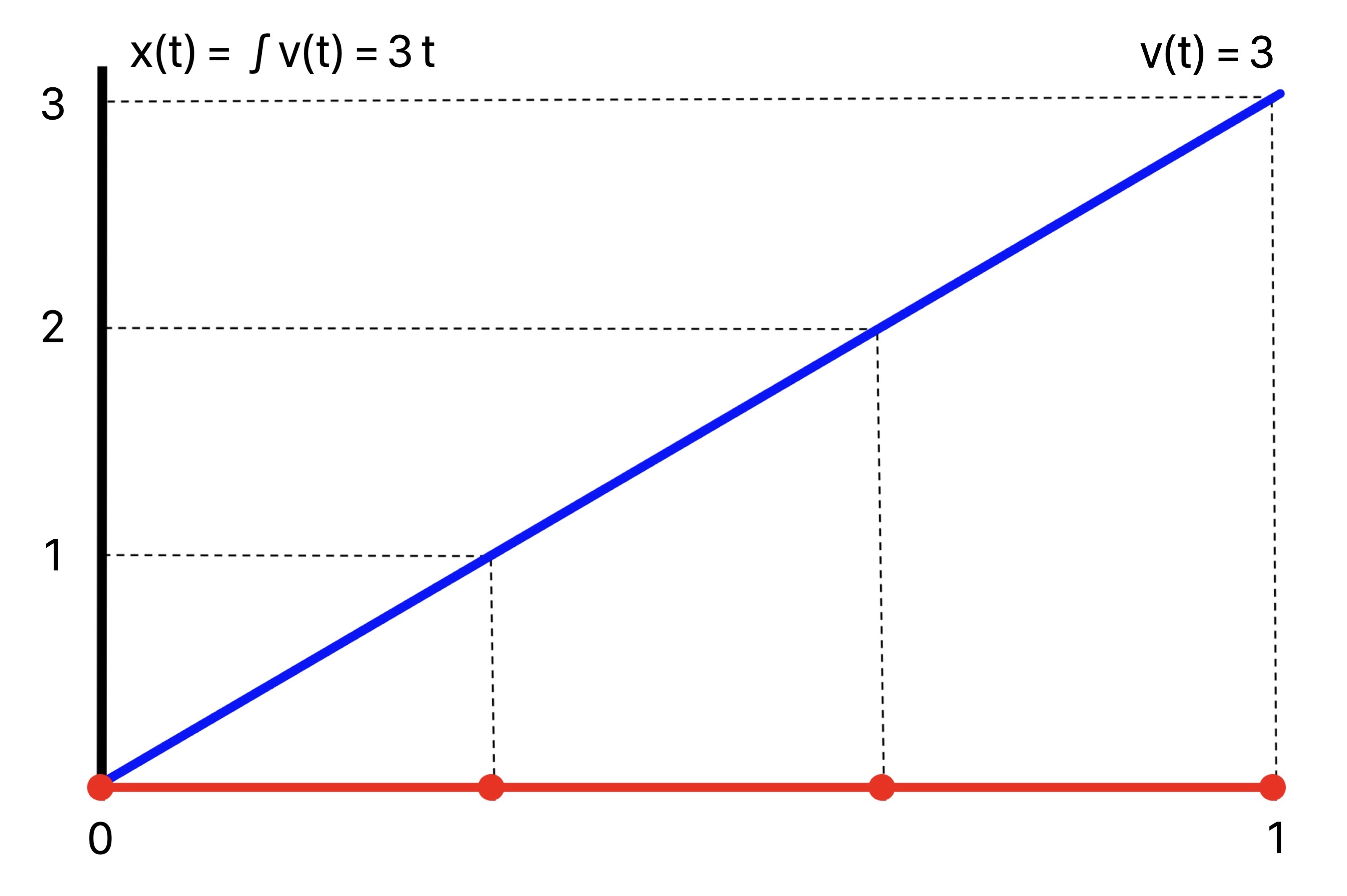
Composing the unit sine wave sin(2 π t) with this argument, plot of sin(2 π (3 t)):
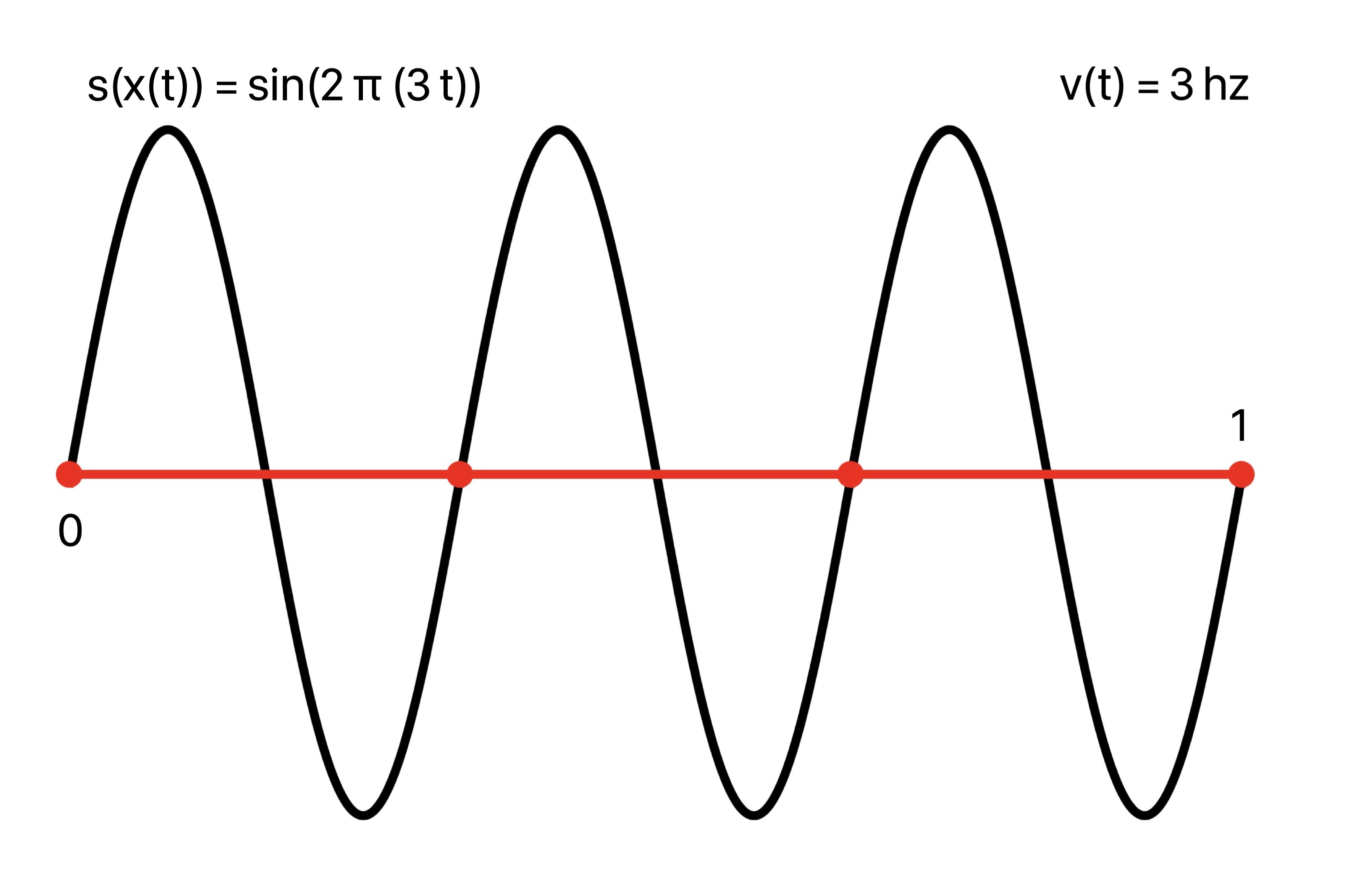
2. Variable Instantaneous Frequency
On the other hand, for variable speed proportional to t, v(t) = t, the periods of sin(2 π t) are traversed at an increasing rate, or increasing frequency. This is seen in the composed plot sin(2 π x(t)) = sin(2 π (t^2 / 2)) with more closely spaced crests as time goes on.
The instantaneous frequency is v(t) = t, with argument given by the antiderivative x(t) = t^2 / 2:
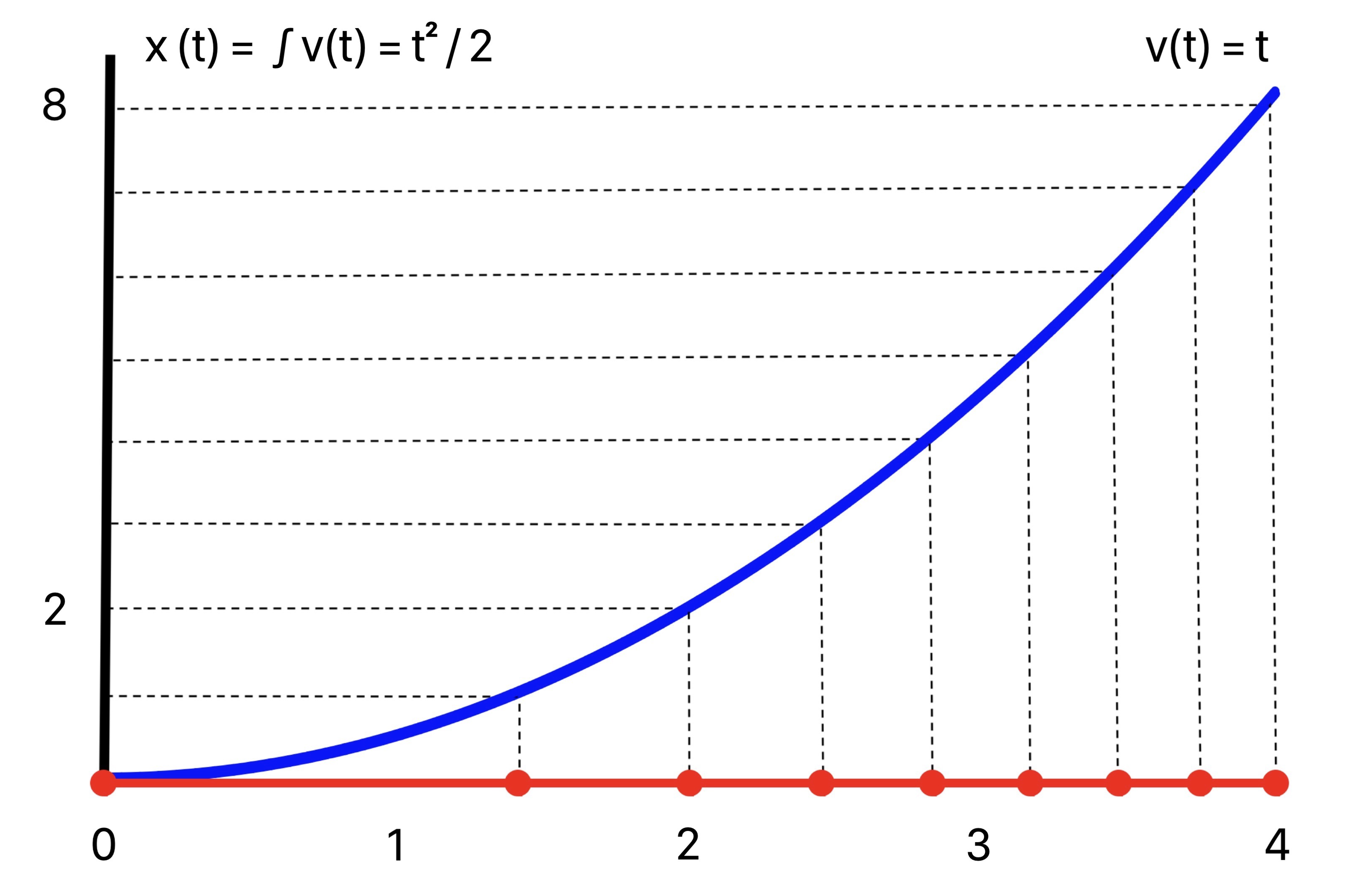
Composing the unit sine wave sin(2 π t) with this argument, plot of sin(2 π (t^2 / 2)):
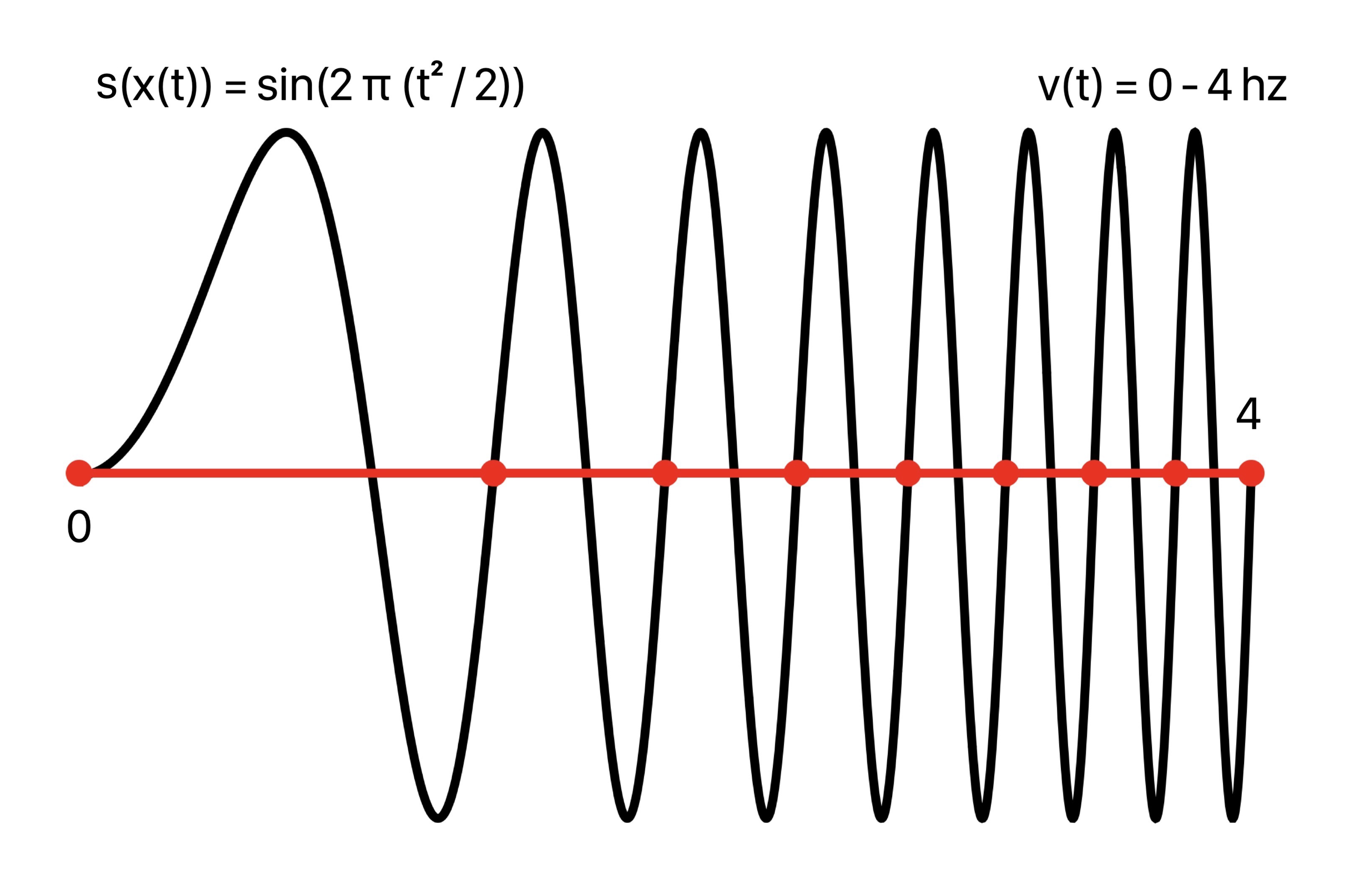
Frequency Ramp
The discussion of Instantaneous Frequency stated a signal s(x(t)) with specific variable frequency can be created by specifying the rate of change function v(t) appropriately, and the argument x(t) is obtained by integration. This is applied here to play the audio for a transition between frequencies when the frequency slider is changed.
When the frequency is changed to v2 the next sample buffer for the current signal s(t) will reflect this change from the previous frequency v1. If the current sample buffer represents an interval of time [t1, t2] then v(t) is derived using linear interpolation to create a ramp between the pair of points (t1, v1) and (t2, v2). Then x(t) = ∫ v(t), and sampling is performed with s(x(t)).
Consider the geometry for this linear interpolation:
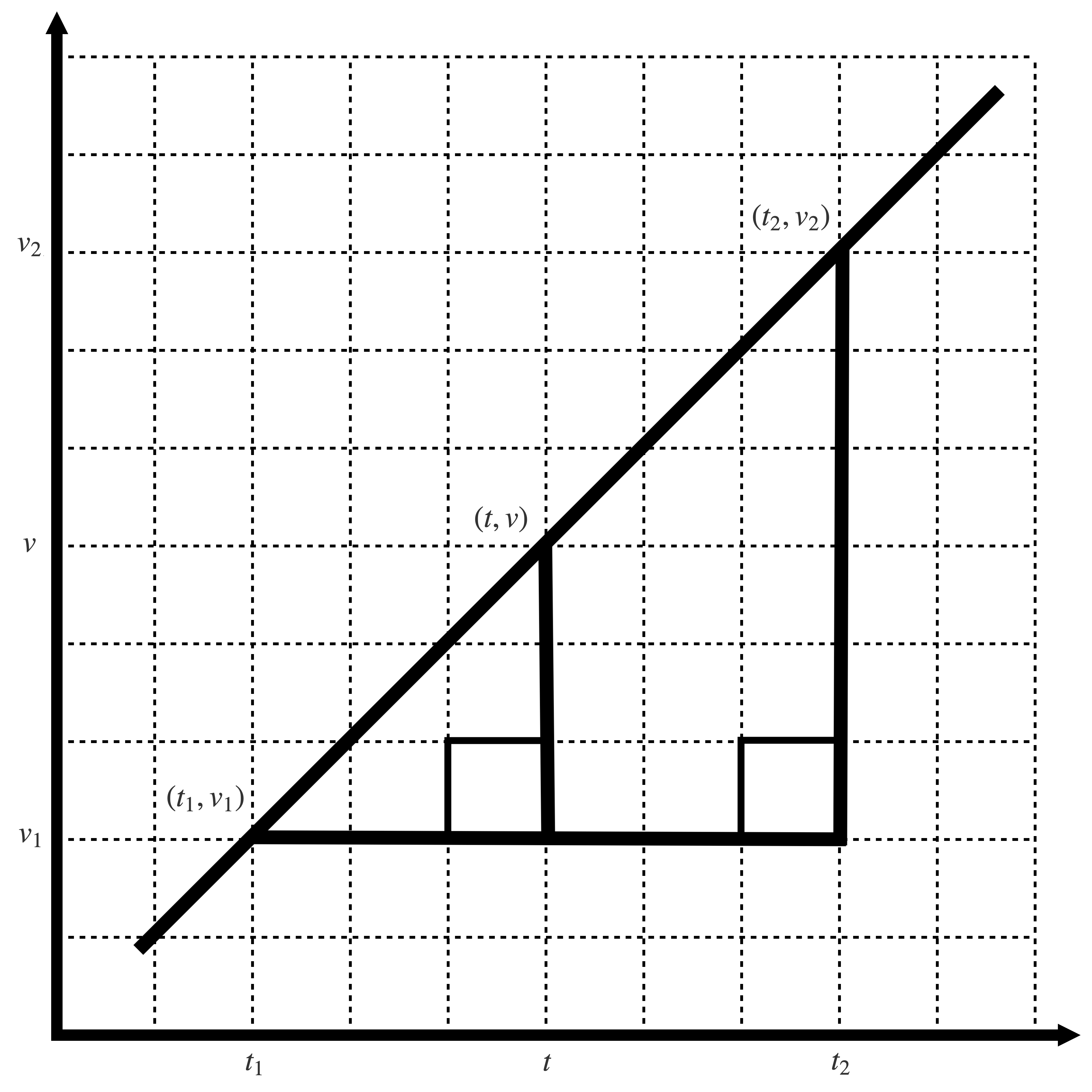
The interpolation relation is given by the similar right triangles:
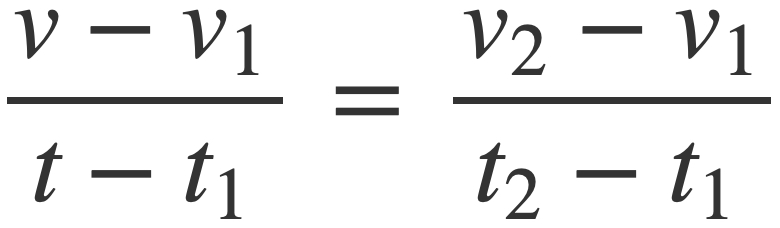
Solving for v(t), or dx/dt, produces the desired frequency ramp:
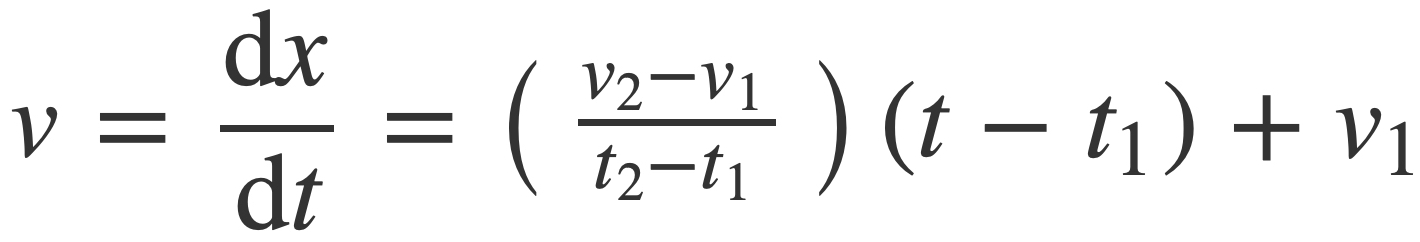
The antiderivative of v, or the signal argument x(t), up to an added constant c is given by:
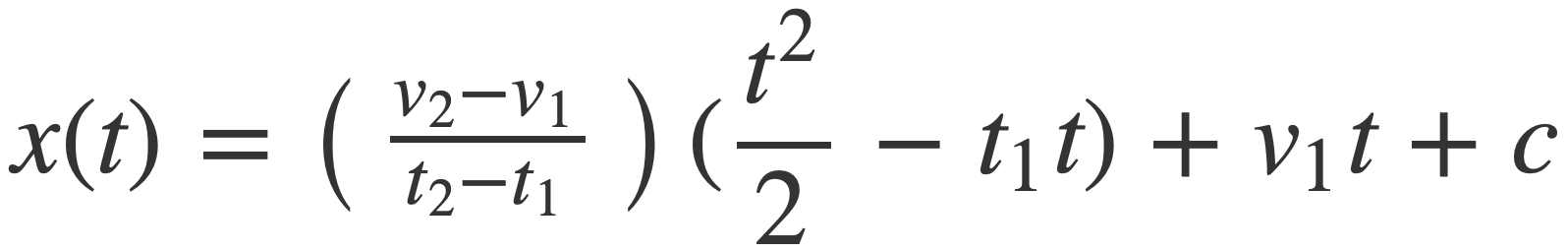
Since the audio signal is invariant under translation c it may be set to zero, and s(x(t) is a function whose frequency changes from v1 to v2 in the time interval [t1,t2].
When v1 = v2 = f, then x(t) = f * t. For the unit function sin(2 π t), substituting f t for t yields the signal sin(2 π f t), which is the familiar form of a sine wave with constant frequency f Hz.
In the general case then sin(2 π x(t)) can be written as sin(2 π g(t) t) when x(t) is factored by pulling out the common factor t:
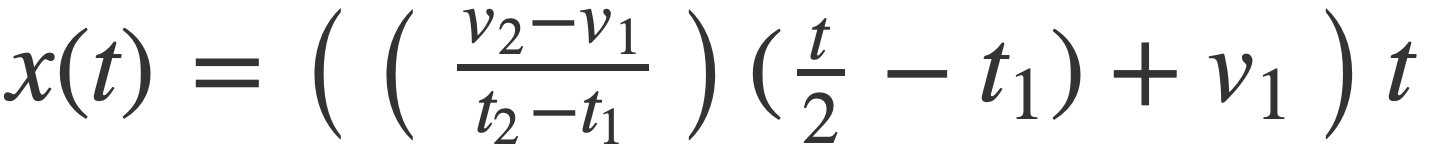
with g(t) given by:
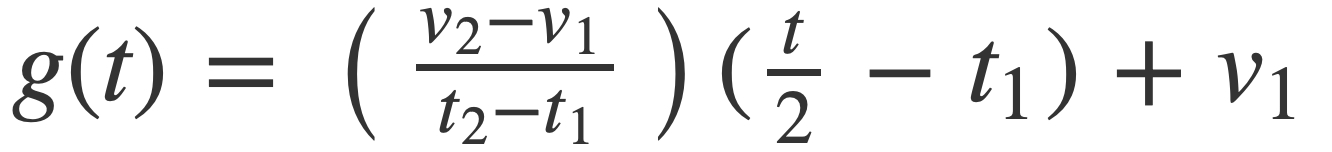
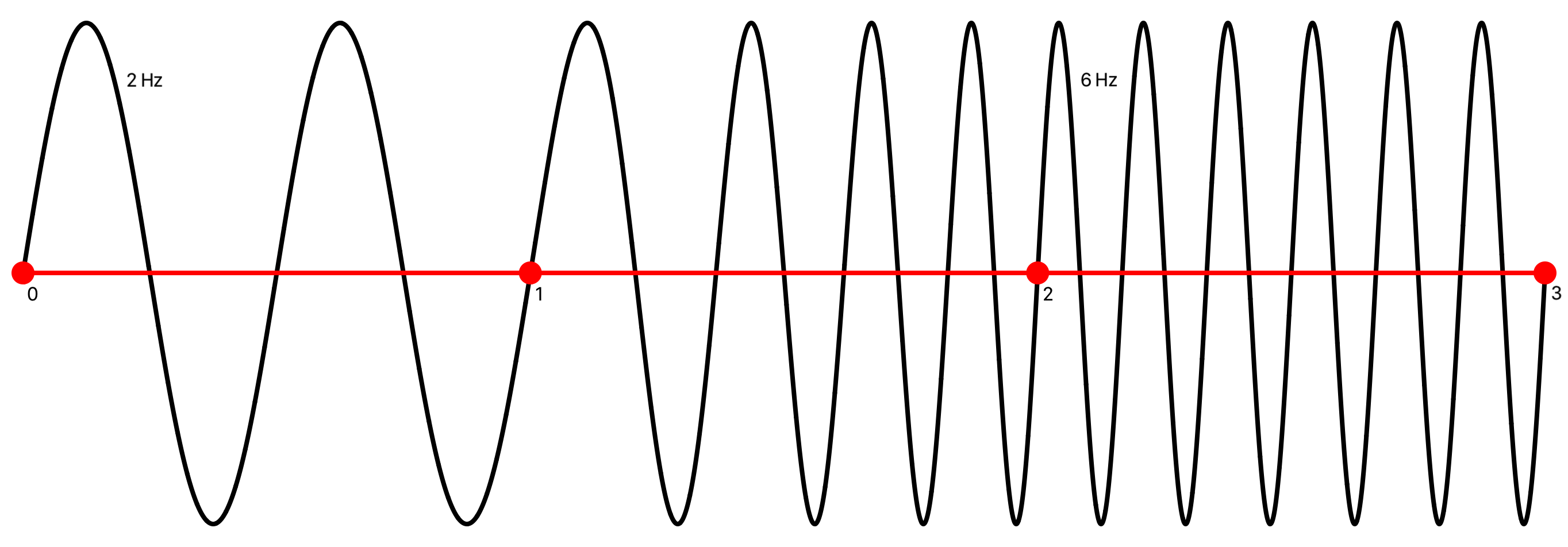
Example. Using these equations a signal that transitions from 2 to 6 Hz on the time interval [1,2] is given by
sin(2 π g(t) t)
where
g(t) = 4 (t / 2 - 1) + 2 = 2 (t - 1)
Check:
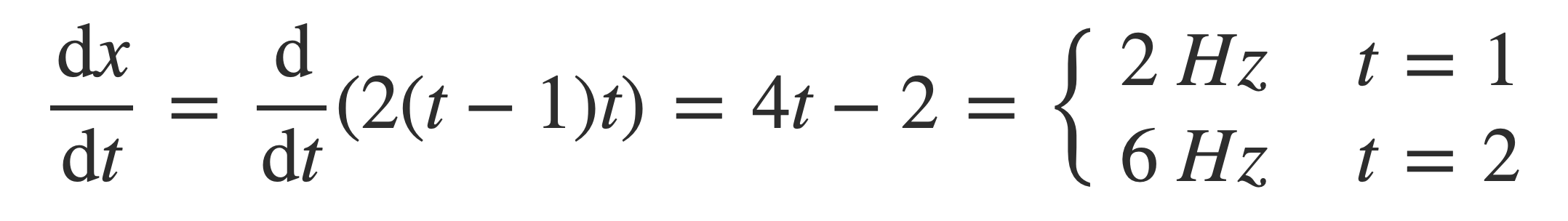
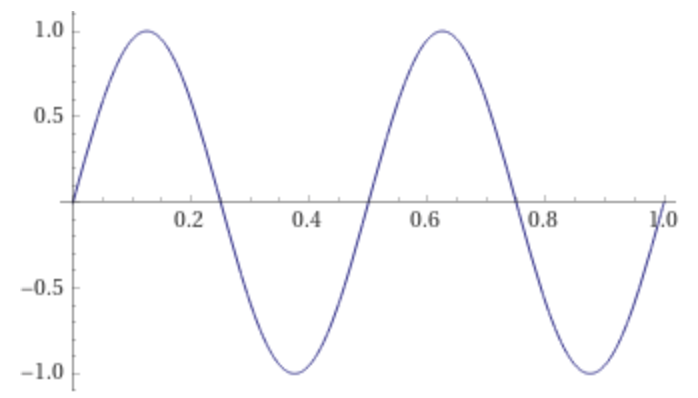
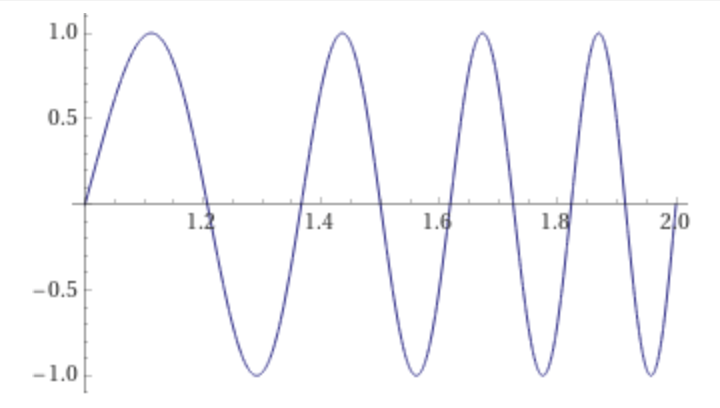
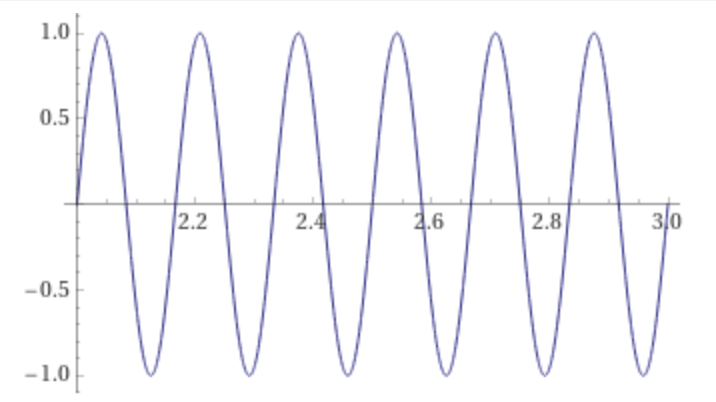
Combining this frequency ramp with a 2 Hz signal sin(2 π 2 t) and a 6 Hz signal sin(2 π 6 t), a piecewise signal is formed:
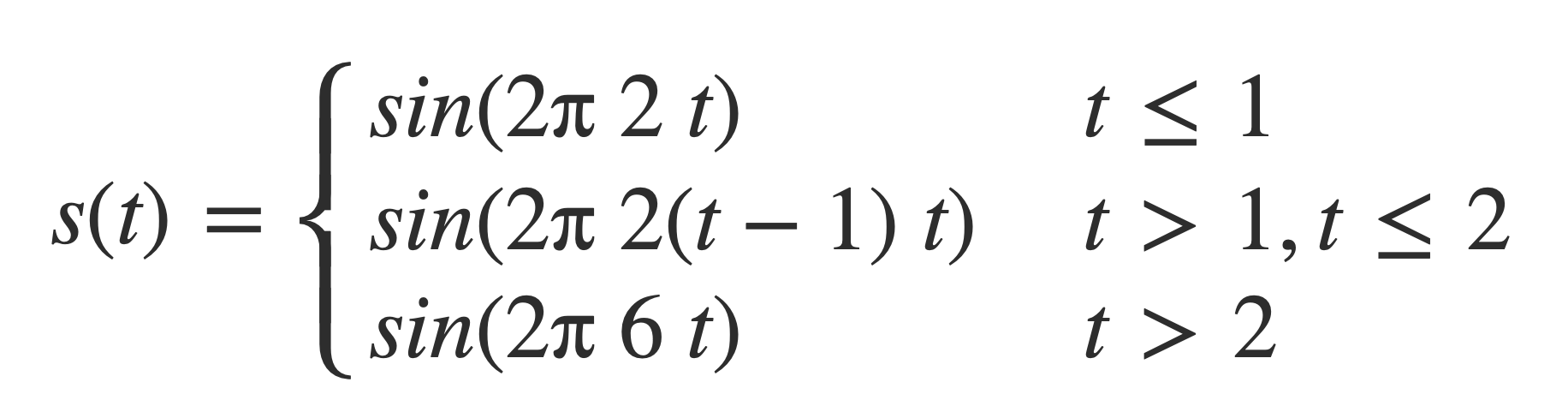
This signal is initially 2 Hz on the interval [0,1], transitions from 2 to 6 Hz on the interval [1,2], and remains 6 Hz on [2,3]:
Plot the parts of the piecewise signal s(t) individually:
plot sin(2 π 2 t) on 0,1
plot sin(2 π 2(t-1) t) on 1,2
plot sin(2 π 6 t) on 2,3
Unit Functions
Unit function types are defined by the WaveFunctionType enumeration, corresponding to unit functions (_ t:Double) -> Double on [0,1] for defining periodic signals with period 1. Signals with other oscillatory frequencies, or periods, are generated with the unit functions by scaling time.
// Note : wavefunctions should have values <= 1.0, otherwise they are clipped in sample generation
// Partial sum value of the Fourier series can exceed 1
enum WaveFunctionType: String, Codable, CaseIterable, Identifiable {
case sine = "Sine"
case square = "Square"
case squareFourier = "Square Fourier"
case triangle = "Triangle"
case triangleFourier = "Triangle Fourier"
case sawtooth = "Sawtooth"
case sawtoothFourier = "Sawtooth Fourier"
var id: Self { self }
}
These are the periodic functions sampled to fill audio sample buffers requested by AVAudioEngine, or to generate WAV file with ToneWriter class method saveComponentSamplesToFile.
A tone is defined with a struct Component.
struct Component {
var type:WaveFunctionType
var frequency:Double
var amplitude:Double
var offset:Double
func value(x:Double) -> Double {
return wavefunction(x, frequency, amplitude, offset, type)
}
}
The unit function for the type is provide by the unitFunction lookup function.
func unitFunction( _ type: WaveFunctionType) -> ((Double)->Double) {
switch type {
case .sine:
return sine(_:)
case .square:
return square(_:)
case .triangle:
return triangle(_:)
case .sawtooth:
return sawtooth(_:)
case .squareFourier:
return { t in square_fourier_series(t, fouierSeriesTermCount) }
case .triangleFourier:
return { t in triangle_fourier_series(t, fouierSeriesTermCount) }
case .sawtoothFourier:
return { t in sawtooth_fourier_series(t, fouierSeriesTermCount) }
}
}
The value of a component is computed by wavefunction using truncatingRemainder to extend to the positive real line the unit function returned by the unitFunction lookup function.
func wavefunction(_ t:Double, _ frequency:Double, _ amplitude:Double, _ offset:Double, _ type: WaveFunctionType) -> Double {
let x = frequency * t + offset
let p = x.truncatingRemainder(dividingBy: 1)
return amplitude * unitFunction(type)(p)
}
Sine Wave
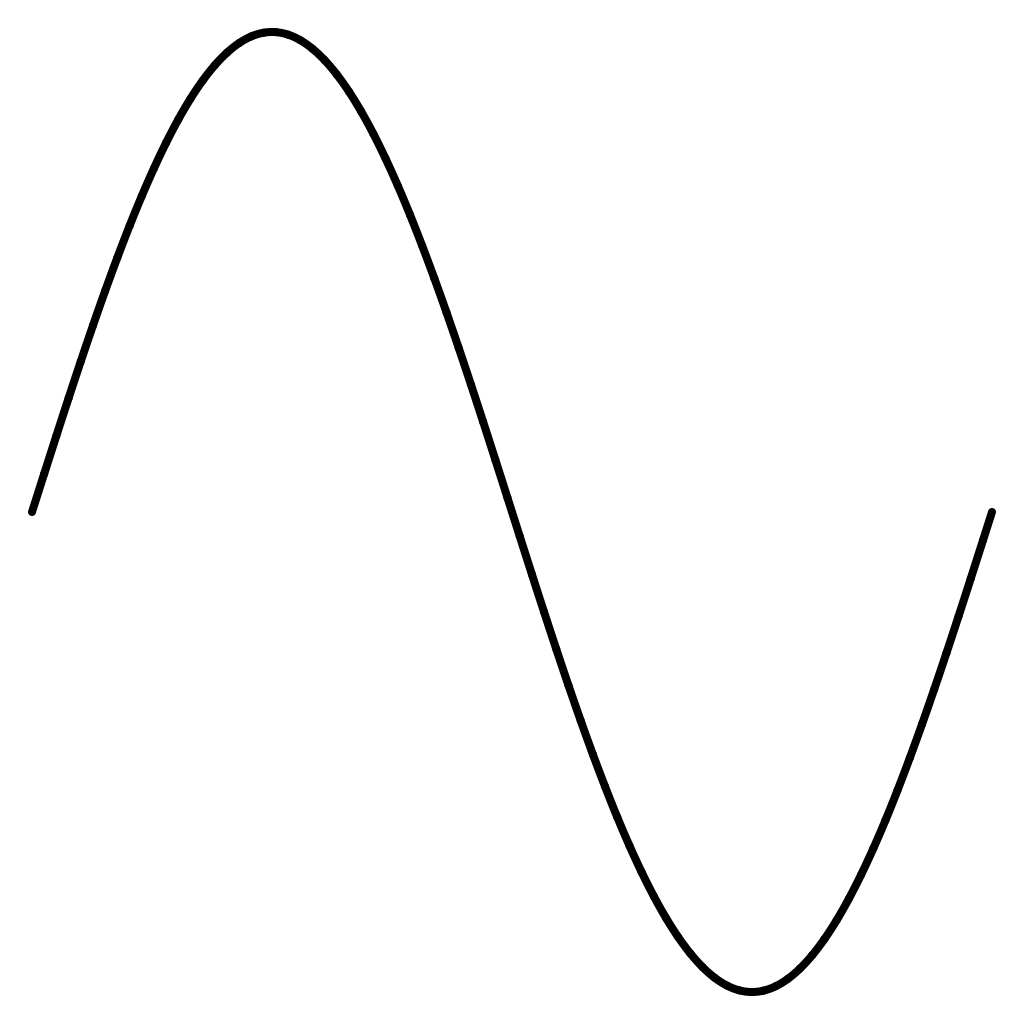
The wave function type .sine is defined on [0,1] with:
func sine(_ t:Double) -> Double {
return sin(2 * .pi * t)
}
Square Wave

The wave function type .square is defined on [0,1] with:
func square(_ t:Double) -> Double {
if t < 0.5 {
return 1
}
return -1
}
Triangle Wave
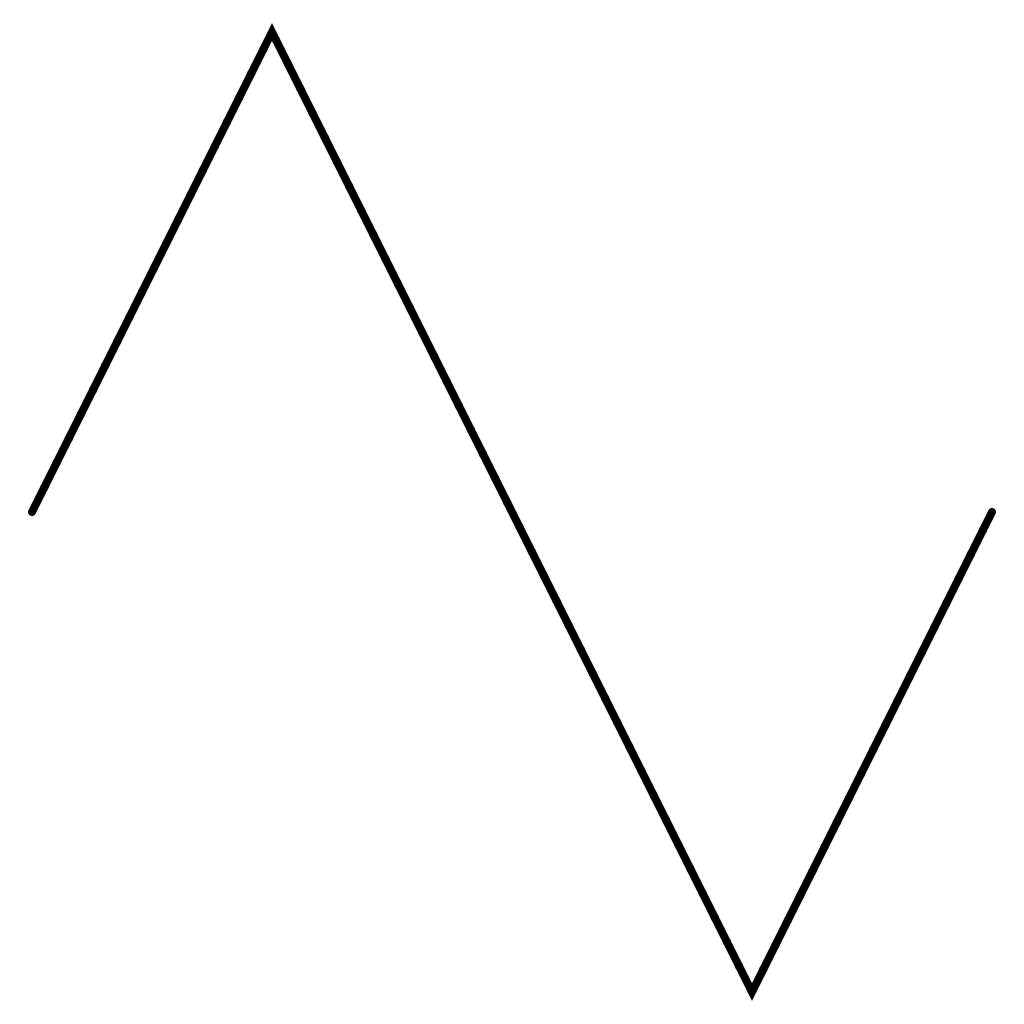
The wave function type .triangle is defined on [0,1] with:
func triangle(_ t:Double) -> Double {
if t < 0.25 {
return 4 * t
}
else if t >= 0.25 && t < 0.75 {
return -4 * t + 2
}
return 4 * t - 4
}
Sawtooth Wave

The wave function type .sawtooth is defined on [0,1] with:
func sawtooth(_ t:Double) -> Double {
return t
}
ToneShaper Fourier series
For each of the signal types square, sawtooth and triangle a partial Fourier series is computed as an alternative signal type. The formula implemented are described in Fourier series at MathWorld.
Periodic functions can be expressed as infinite sums of sine and cosine waves using Fourier series. Truncated Fourier series of the unit functions .square, .triangle and .sawtooth are provided for comparison.
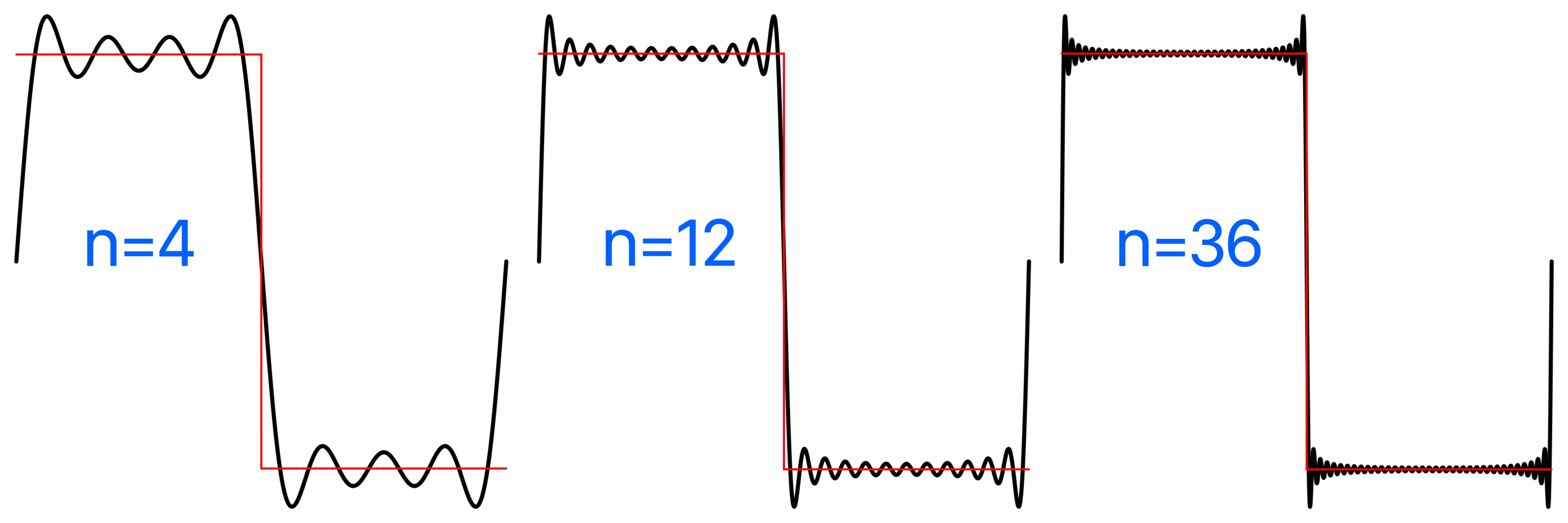
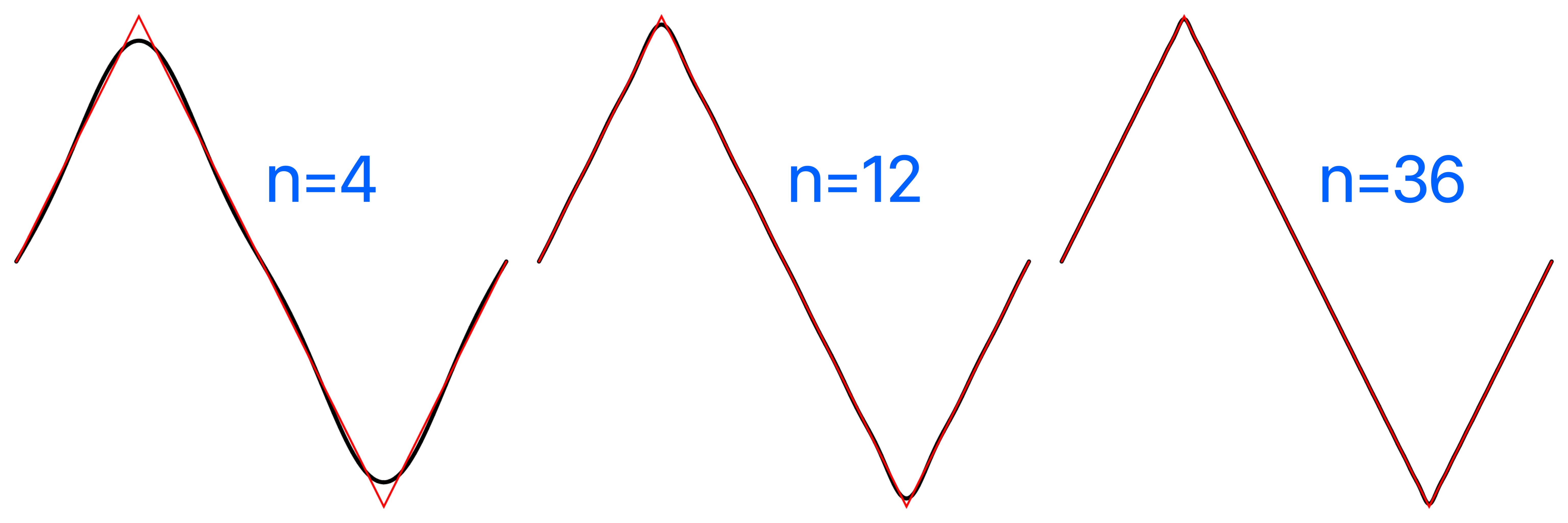
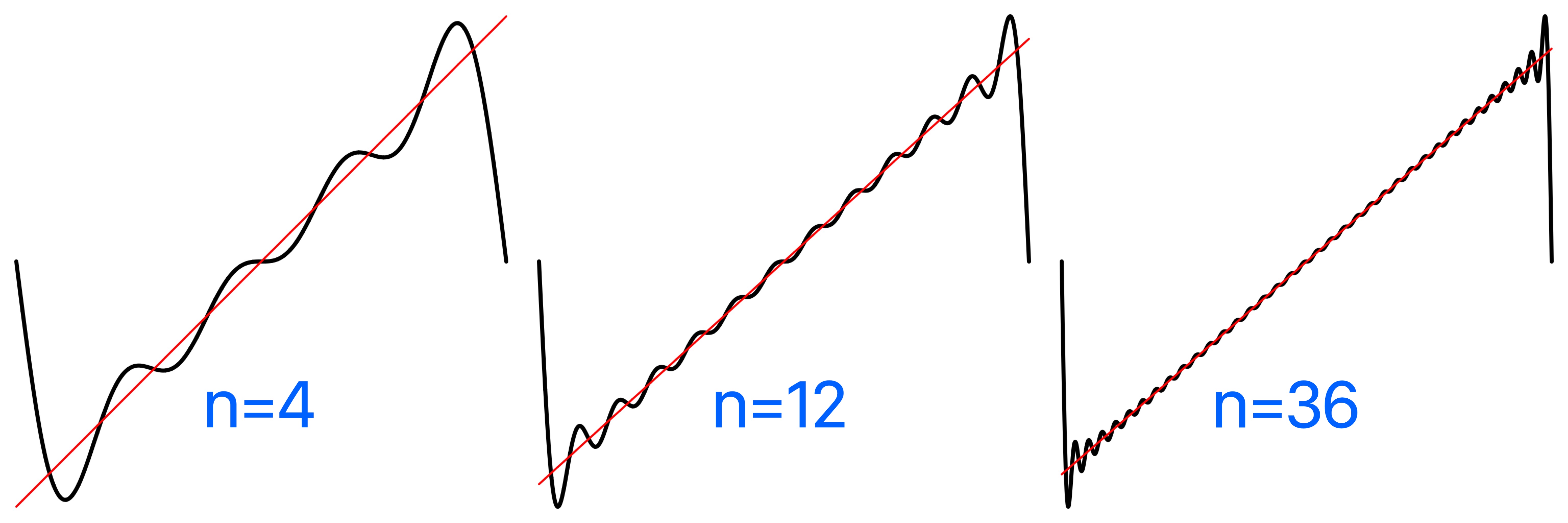
For a differentiable function with discontinuities, such as the square and sawtooth, the Fourier series partial sums converge to the function at points where it is differentiable, but always exhibit significant approximation error near any discontinuity, referred to as Gibbs phenomenon.
In the implementation wave functions should have values ≤ 1.0 as they are converted to Int16 values, but the partial sums of the Fourier series can exceed 1. Values > 1 are clipped during sampling since Int16 audio samples are bounded to the range Int16.min...Int16.max = -32768...32767.
Square Fourier
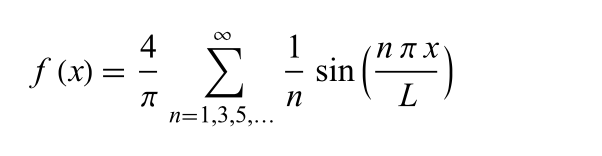
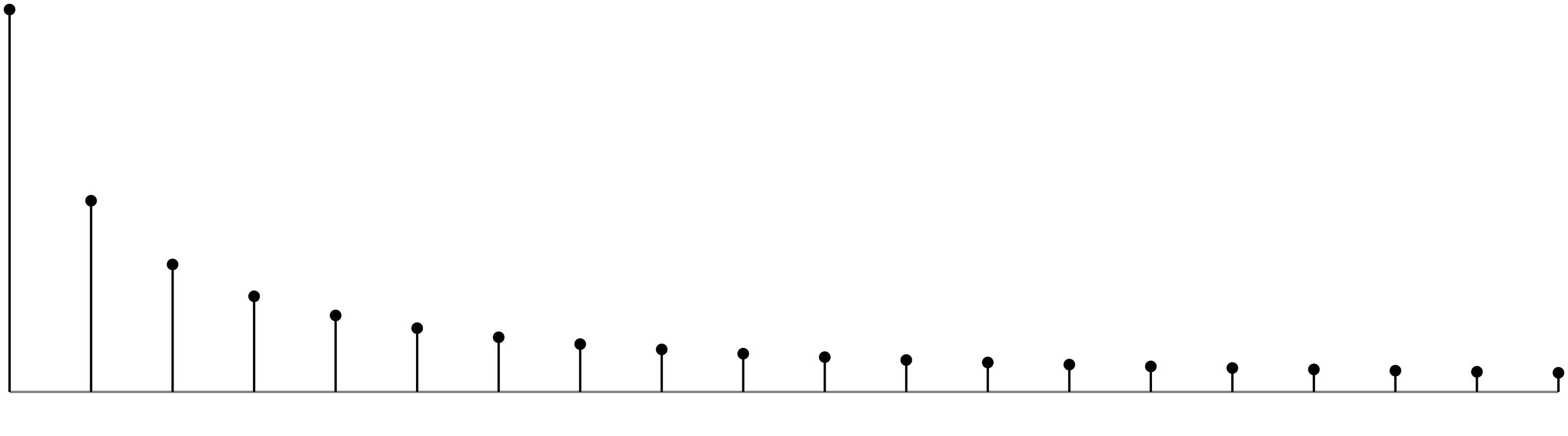
See Square Wave Fourier series for a derivation of this formula, with L=½ for the Square unit function.
square_fourier_series implements this formula where n is the desired number of terms.
func square_fourier_series(_ t:Double, _ n:Int) -> Double {
var sum = 0.0
for i in stride(from: 1, through: n * 2, by: 2) {
let a = Double(i)
sum += ((1.0 / a) * sin(2 * a * .pi * t))
}
return (4.0 / .pi) * sum
}
Plot of the square Fourier series comparatively using square_fourier_series, the square wave plotted in red, the Fourier series in black. For a differentiable function with discontinuities, such as the square and sawtooth, the Fourier series partial sums converge to the function at points where it is differentiable, but always exhibit significant approximation error near the discontinuity, referred to as Gibbs phenomenon.
Square Wave Fourier Coefficients:

Triangle Fourier
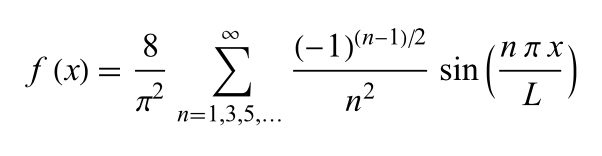
See Triangle Wave Fourier series for a derivation of this formula, with L=½ for the Triangle unit function.
triangle_fourier_series implements this formula where n is the desired number of terms.
func triangle_fourier_series(_ t:Double, _ n:Int) -> Double {
var sum = 0.0
for i in stride(from: 1, through: n, by: 2) {
let a = Double(i)
sum += ((pow(-1,(a-1)/2) / pow(a, 2.0)) * sin(2 * a * .pi * t))
}
return (8.0 / pow(.pi, 2.0)) * sum
}
Plot of the triangle Fourier series comparatively using triangle_fourier_series, the triangle wave plotted in red, the Fourier series in black.
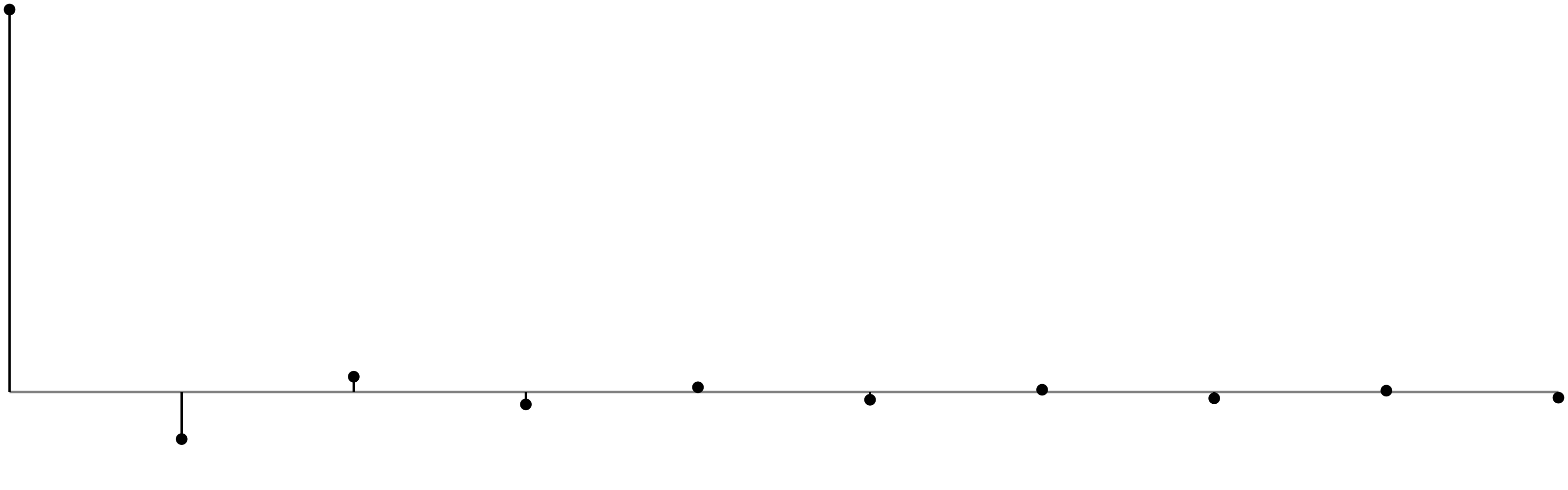
Triangle Wave Fourier Coefficients:
Sawtooth Fourier
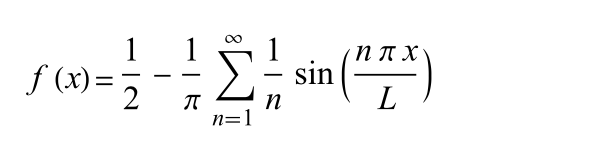
See Sawtooth Wave Fourier series for a derivation of this formula, with L=½ for the Sawtooth unit function.
sawtooth_fourier_series implements this formula where n is the desired number of terms.
func sawtooth_fourier_series(_ t:Double, _ n:Int) -> Double {
var sum = 0.0
for i in 1...n {
sum += sin(Double(i) * 2.0 * .pi * t) / Double(i)
}
return 0.5 + (-1.0 / .pi) * sum
}
Plot of the sawtooth Fourier series comparatively using sawtooth_fourier_series, the sawtooth wave plotted in red, the Fourier series in black. For a differentiable function with discontinuities, such as the square and sawtooth, the Fourier series partial sums converge to the function at points where it is differentiable, but always exhibit significant approximation error near the discontinuity, referred to as Gibbs phenomenon.
Sawtooth Wave Fourier Coefficients:
Writing Tone Files
A tone defined by a Component can be written to a WAV file of specified duration with the ToneWriter class method toneWriter.saveComponentSamplesToFile that uses AVFoundation to write audio sample buffers.
var testToneWriter = ToneWriter()
func TestToneWriter(wavetype: WaveFunctionType, frequency:Double, amplitude: Double, duration: Double, scale: ((Double)->Double)? = nil) {
if let documentsURL = FileManager.documentsURL(filename: nil, subdirectoryName: nil) {
print(documentsURL)
let destinationURL = documentsURL.appendingPathComponent("tonewriter - \(wavetype), \(frequency) hz, \(duration).wav")
testToneWriter.scale = scale
testToneWriter.saveComponentSamplesToFile(component: Component(type: wavetype, frequency: frequency, amplitude: amplitude, offset: 0), duration: duration, destinationURL: destinationURL) { resultURL, message in
if let resultURL = resultURL {
#if os(macOS)
NSWorkspace.shared.open(resultURL)
#endif
let asset = AVAsset(url: resultURL)
Task {
do {
let duration = try await asset.load(.duration)
print("ToneWriter : audio duration = \(duration.seconds)")
}
catch {
print("\(error)")
}
}
}
else {
print("An error occurred : \(message ?? "No error message available.")")
}
}
}
}
In GenerateTonePlayerSample the ToneWriter is used to create this audio file sample:
The duration is calculated for the time at which the signal has decayed to effectively zero:
/*
Solve for t: e^(-2t) = 1/Int16.max, smallest positive value of Int16 (where positive means > 0)
*/
func GenerateTonePlayerSample() {
let D = -log(1.0/Double(Int16.max)) / 2.0 // D = 5.198588595177692
print(D)
let scale:((Double)->Double) = {t in exp(-2 * t)}
TestToneWriter(wavetype: .sine, frequency: 440, amplitude: 1, duration: D, scale: scale)
}
Interpolating Instantaneous Frequency
An array of instantaneous frequency values v(t) is integrated to produce the argument x(t) of the current periodic signal s(t) that is a Unit Function, or its Fourier series counterpart.
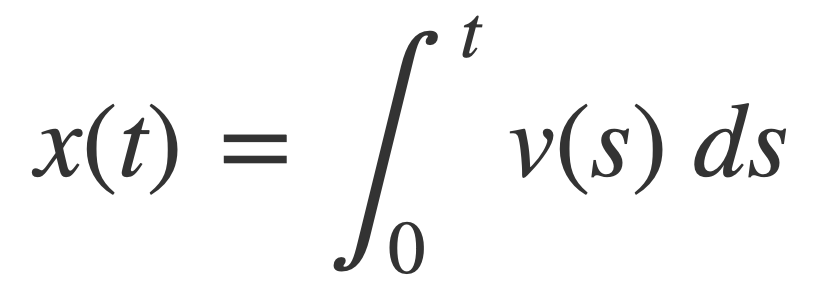
The composition s(x(t)) is sampled to create audio sample buffers that can be played with AVAudioEngine or saved to files with ToneWriter.
A user selects an audio duration and frequency range, then draws a curve specifying the shape of instantaneous frequency in a View using tap or drag gestures. This curve is drawn in view coordinate space with the view width as the time domain and its height as the frequency range. The view coordinates of the gestures are then mapped with an affine mapping into an array points:[CGPoint] in the model coordinate space, where a points x-coordinate corresponds to an actual time within the selected duration of the audio, and its y-coordinate represents the actual instantaneous frequency at that time within the selected frequency range. The user points along with selected duration and frequency range are stored in a document so that they can be restored when it is opened.
The model points are scaled to an array userIFCurve:[CGPoint] whose x-coordinates are integers in an interval [0,N], for an some integer N > 0, a variable value that can affect the sound:
func userIFCurve(_ N:Int, points:[CGPoint]) -> [CGPoint] {
guard let firstPoint = points.first, let lastPoint = points.last else {
return []
}
let minX = firstPoint.x
let maxX = lastPoint.x
let scaleFactor = CGFloat(N) / (maxX - minX)
// Map the points to integers in the [0, N] interval
let scaledPoints = points.map { point in
let scaledX = Int((point.x - minX) * scaleFactor)
return CGPoint(x: CGFloat(scaledX), y: point.y)
}
return scaledPoints
}
To specify an instantaneous frequency value for every audio sample, the userIFCurve is extended by interpolation with vDSP.linearInterpolate to produce an array of instantaneous frequency values, sampleIFValues. The number of audio samples, sampleCount, is determined by the desired duration and sample rate:
sampleCount = Int(duration * Double(sampleRate))
The scale factor is then calculated:
func scale(sampleCount:Int, userIFCurve:[CGPoint]) -> Double {
Double(sampleCount-1) / userIFCurve.last!.x
}
The scale factor is chosen to map the last userIFCurve index (x-coordinate), userIFCurve.last!.x, to the last index of the array of audio samples, Double(sampleCount-1):
scale * userIFCurve.last!.x = Double(sampleCount-1)
Extending the user curve to the entire set of audio samples can be achieved either comprehensively in one step or incrementally through a piecewise approach, depending on specific requirements.
Complete Interpolation with vDSP
Interpolating Instantaneous Frequency ↑
Instantaneous frequency values for all audio samples can be calculated at once from the userIFCurve with linear interpolation using allSampleIFValues_by_interpolateUserIFCurve:
let allSampleIFValues = allSampleIFValues_by_interpolateUserIFCurve(sampleCount: sampleCount, userIFCurve: userIFCurve)
The vDSP.linearInterpolate function is applied using the integer valued x-coordinates of the userIFCurve as indices for interpolating the frequency values of the y-coordinates:
func allSampleIFValues_by_interpolateUserIFCurve(sampleCount:Int, userIFCurve:[CGPoint]) -> ([Double], [Double]) {
let userIFIndices = userIFCurve.map { Double($0.x) }
let userIFValues = userIFCurve.map { Double($0.y) }
let scale = scale(sampleCount: sampleCount, userIFCurve: userIFCurve)
let sampleIFIndices = userIFIndices.map { ($0 * scale).rounded() }
return (vDSP.linearInterpolate(values: userIFValues, atIndices: sampleIFIndices), sampleIFIndices)
}
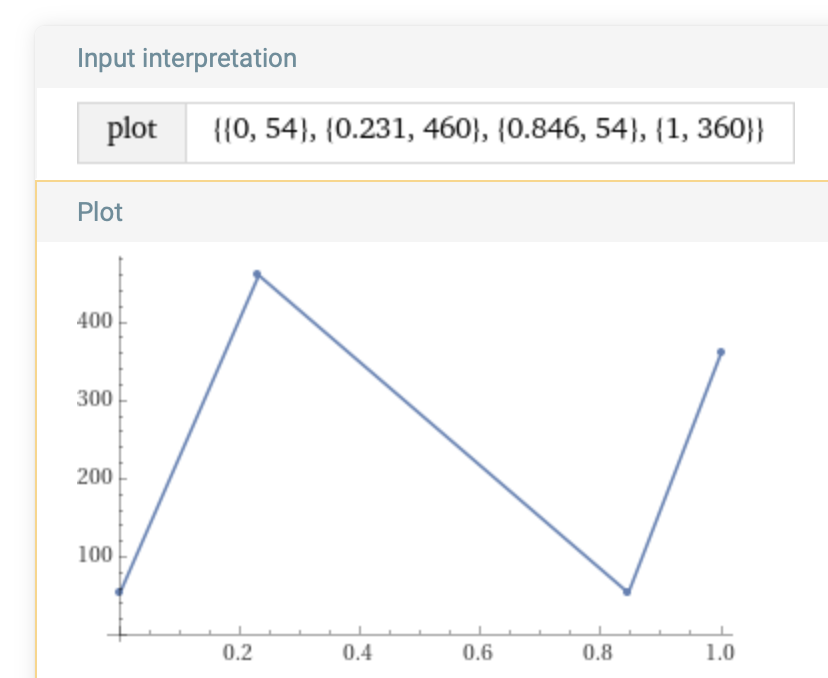
Time-Frequency coordinates are represented using CGPoint so that they can be selected and drawn in a View using a Path. The x-coordinate is time, and the y-coordinate is frequency. For example, these tuples as x and y-coordinates
(0.0, 54.0), (0.231, 460.0), (0.846, 54.0), (1.0, 360.0)
can be converted to an array of CGPoint:
let points:[CGPoint] = [(0.0, 54.0), (0.231, 460.0), (0.846, 54.0), (1.0, 360.0)].map { CGPoint(x: CGFloat($0.0), y: CGFloat($0.1)) }
The interpretation of this set of points is a tone shape of 1 second duration, because the start time is
points[0].x = 0,
and end time is
points[3].x = 1.
The first point (0.0, 54.0) indicates that at time 0.0 seconds the frequency will be 54.0 Hz, and the second point (0.231, 460.0) indicates that at time 0.231 seconds the frequency will be 460.0 Hz. Then at all times in between 0.0 and 0.231 the frequency will be determined by the line that joins these two points in the plane creating a frequency ramp between these points. This is how frequency values are assigned to all audio samples while preserving the shape of the users curve. When the number of samples is very large the Accelerate framework function vDSP.linearInterpolate can be used. If the audio sample rate is 44100 Hz, then every second of audio has 44100 samples, and each of these samples, indexed from 0 to (44100-1), is assigned a frequency value using linear interpolation.
Use the following expression in WolframAlpha to plot the points above:
plot [(0.0, 54.0), (0.231, 460.0), (0.846, 54.0), (1.0, 360.0)]
With vDSP.linearInterpolate these 4 points can be interpolated to create an array of frequency at 36 points as follows:
func interpolation_with_vDSP() {
let userIFCurvePointCount = 500
let points:[CGPoint] = [(0.0, 54.0), (0.231, 460.0), (0.846, 54.0), (1.0, 360.0)].map { CGPoint(x: CGFloat($0.0), y: CGFloat($0.1)) }
let userIFCurve = userIFCurve(userIFCurvePointCount, points: points)
let sampleIFValues = allSampleIFValues_by_interpolateUserIFCurve(sampleCount: 36, userIFCurve: userIFCurve).0
let sampleIFValuesRounded = sampleIFValues.compactMap { value in
Int(value.rounded())
}
print("points = \(points)\n")
print("userIFCurve = \(userIFCurve)\n")
print("sampleIFValuesRounded = \(sampleIFValuesRounded)\n")
}
Download and run the associated playground, executing:
interpolation_with_vDSP()
This prints:
points = [(0.0, 54.0), (0.231, 460.0), (0.846, 54.0), (1.0, 360.0)]
userIFCurve = [(0.0, 54.0), (115.0, 460.0), (423.0, 54.0), (500.0, 360.0)]
sampleIFValuesRounded = [54, 105, 156, 206, 257, 308, 359, 409, 460, 442, 423, 405, 386, 368, 349, 331, 312, 294, 275, 257, 239, 220, 202, 183, 165, 146, 128, 109, 91, 72, 54, 115, 176, 238, 299, 360]
The interpolated values were rounded to nearest integer to decrease the amount of text input for the comparison plot of sampleIFValuesRounded with this expression:
plot 54, 105, 156, 206, 257, 308, 359, 409, 460, 442, 423, 405, 386, 368, 349, 331, 312, 294, 275, 257, 239, 220, 202, 183, 165, 146, 128, 109, 91, 72, 54, 115, 176, 238, 299, 360
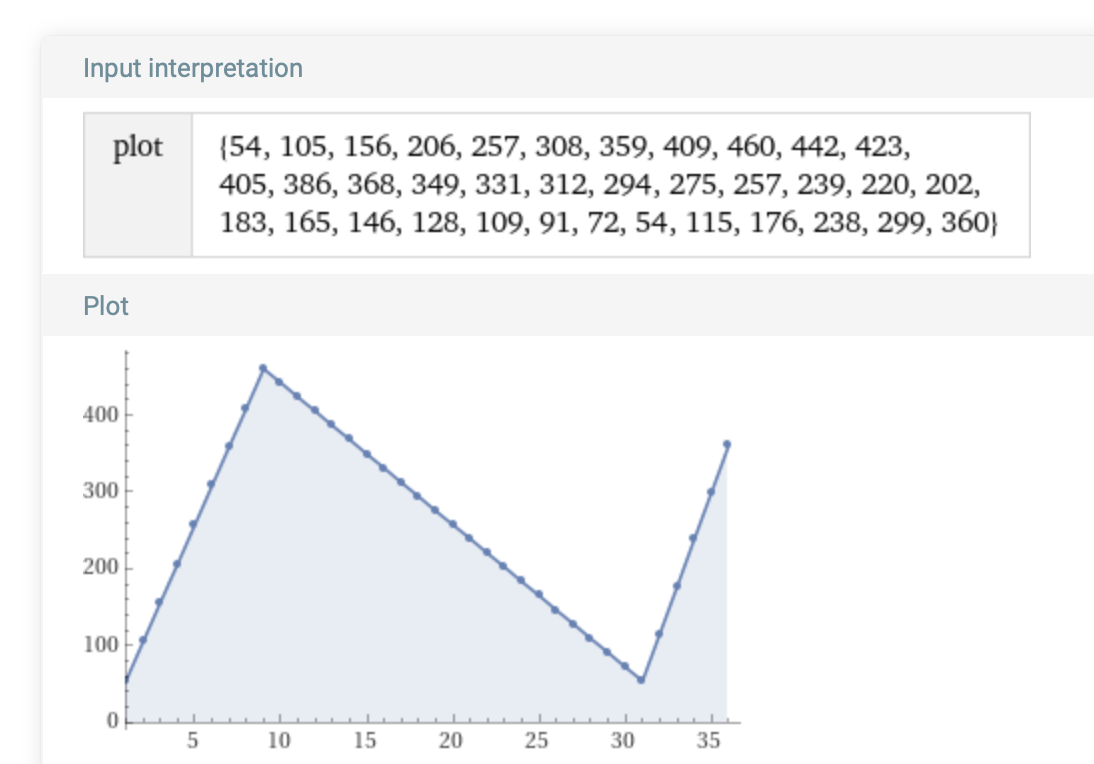
This plot has the same shape as the plot with just four points, but also shows the intermediary points corresponding to interpolated frequency values.
Piecewise Interpolation with vDSP
Interpolating-Instantaneous-Frequency ↑
The preferred implementation does not calculate all the instantaneous frequency at once, but produces instantaneous frequency values per buffer using a method called piecewise interpolation. Piecewise interpolation is used later to implement piecewise integration of the instantaneous frequency function v(t).
Since audio is played and written as a series of audio sample buffers the generation of instantaneous frequency values is actually performed as sample buffers are required. For that there is the function sampleIFValuesForRange, that returns interpolated values in a ClosedRange of Int that specifies current the sample buffer indices:
func sampleIFValuesForRange(scale:Double, sampleRange:ClosedRange<Int>, userIFValues:[Double]) -> [Double]
For an example how audio samples are packaged into sample buffers and written to files see the ToneWriter.swift source code. For an overview of how sample buffers are played with AVAudioEngine see Tone Generation.
To illustrate the process for a sample count of 15, first compute all 15 instantaneous frequency values at once, similarly to what was computed in Complete Interpolation with vDSP.
The following helper functions is in the associated playground:
func userIFValues_by_interpolateUserIFCurve(userIFCurve:[CGPoint]) -> [Double] {
let indices = userIFCurve.map { Double($0.x) }
let values = userIFCurve.map { Double($0.y) }
return vDSP.linearInterpolate(values: values, atIndices: indices)
}
extension Double {
func roundTo(_ places:Int) -> Double {
let divisor = pow(10.0, Double(places))
return (self * divisor).rounded() / divisor
}
}
Then compute:
let sampleCount = 15
let userIFCurve = [(1.0, 6.3), (3.0, 11.1), (7.0, 2.1)].map { CGPoint(x: CGFloat($0.0), y: CGFloat($0.1)) }
let userIFValues = userIFValues_by_interpolateUserIFCurve(userIFCurve: userIFCurve)
let scaleFactor = scale(sampleCount: sampleCount, userIFCurve: userIFCurve)
// First, generate all sample IF values by directly interpolating userIFCurve with allSampleIFValues_by_interpolateUserIFCurve:
let allSampleIFValues = allSampleIFValues_by_interpolateUserIFCurve(sampleCount: sampleCount, userIFCurve: userIFCurve).0.map { v in
v.roundTo(3)
}
print("userIFCurve = \(userIFCurve)")
print("userIFValues = \(userIFValues)")
print("allSampleIFValues = \(allSampleIFValues)")
Printing values, in particular all 15 values of allSampleIFValues:
userIFCurve = [(1.0, 6.3), (3.0, 11.1), (7.0, 2.1)]
userIFValues = [6.3, 6.3, 8.7, 11.1, 8.85, 6.6, 4.35, 2.0999999999999996]
allSampleIFValues = [6.3, 6.3, 6.3, 7.5, 8.7, 9.9, 11.1, 9.975, 8.85, 7.725, 6.6, 5.475, 4.35, 3.225, 2.1]
Next compute the same using a partition of the full range with the function sampleIFValuesForRange, accumulating the results into allSampleIFValuesPiecewise to compare with allSampleIFValues.
The following helper functions were added to the associated playground:
func createPartitionRanges(sampleCount: Int, rangeCount: Int) -> [ClosedRange<Int>] {
guard rangeCount > 0 else {
return []
}
var ranges: [ClosedRange<Int>] = []
var start = 0
while start < sampleCount {
let end = min(start + rangeCount, sampleCount) - 1
let range = start...end
ranges.append(range)
start = end + 1
}
return ranges
}
func sampleIFValuesForRange(scale:Double, sampleRange:ClosedRange<Int>, userIFValues:[Double]) -> [Double] {
// scale sample range into user range
let ta = Double(sampleRange.lowerBound) / scale
let tb = Double(sampleRange.upperBound) / scale
var valuesToInterpolate:[Double] = []
var sampleIndices:[Double] = []
func appendInterploatedValue(_ t:Double) {
let delta = (t - t.rounded(.down))
let index = Int(t.rounded(.down))
if delta == 0 || (index+1 > userIFValues.count-1) { // index+1 may be out of bounds when delta = 0, or very nearly 0
valuesToInterpolate.append(userIFValues[index])
}
else {
let interpolated = userIFValues[index] * (1 - delta) + userIFValues[index+1] * delta
valuesToInterpolate.append(interpolated)
}
}
if ta == tb {
appendInterploatedValue(ta)
sampleIndices.append(Double(sampleRange.lowerBound))
}
else {
// start
appendInterploatedValue(ta)
sampleIndices.append(Double(sampleRange.lowerBound))
// middle, if any
var lowerBound = Int(ta.rounded(.up))
if lowerBound == Int(ta.rounded(.down)) {
lowerBound += 1
}
var upperBound = Int(tb.rounded(.down))
if upperBound == Int(tb.rounded(.up)) {
upperBound -= 1
}
if lowerBound <= upperBound {
valuesToInterpolate.append(contentsOf: Array(userIFValues[lowerBound...upperBound]))
sampleIndices.append(contentsOf: (lowerBound...upperBound).map { Double($0) * scale })
}
// end
appendInterploatedValue(tb)
sampleIndices.append(Double(sampleRange.upperBound))
}
sampleIndices = sampleIndices.map { $0 - sampleIndices[0]}
return vDSP.linearInterpolate(values: valuesToInterpolate, atIndices: sampleIndices)
}
Then compute:
let range_partition = createPartitionRanges(sampleCount: sampleCount, rangeCount: sampleCount/3)
// Then use the range partition to generate of sample IF values by range, and accumulate them into allSampleIFValuesPiecewise
var allSampleIFValuesPiecewise:[Double] = []
for partition in range_partition {
let sampleIFValuesForRange = sampleIFValuesForRange(scale: scaleFactor, sampleRange: partition, userIFValues: userIFValues).map { v in
v.roundTo(3)
}
allSampleIFValuesPiecewise.append(contentsOf: sampleIFValuesForRange)
}
print("range_partition = \(range_partition)")
print("allSampleIFValuesPiecewise = \(allSampleIFValuesPiecewise)")
The result allSampleIFValuesPiecewise is the same as the previous instantaneous frequency values in allSampleIFValues:
range_partition = [ClosedRange(0...4), ClosedRange(5...9), ClosedRange(10...14)]
allSampleIFValuesPiecewise = [6.3, 6.3, 6.3, 7.5, 8.7, 9.9, 11.1, 9.975, 8.85, 7.725, 6.6, 5.475, 4.35, 3.225, 2.1]
In practice there will be indistinguishable numerical differences between the two methods.
Numerical Integration
The definite integral of a function can be numerically calculated with vDSP_vsimpsD and sampling. A linearly interpolated function defined by the sequence of points userIFCurve drawn by the user will be integrated this way. The integration produces the argument of the chosen component function for sampling, according to the discussion of Instantaneous Frequency. The samples are then used to create audio sample buffers to play with AVAudioEngine or save to a WAV file.
The integration process is examined by applying it to function with a known definite integral. The integral ∫ cos(2πt) can be computed knowing that the derivative of sin(2πt) is 2π cos(2πt):
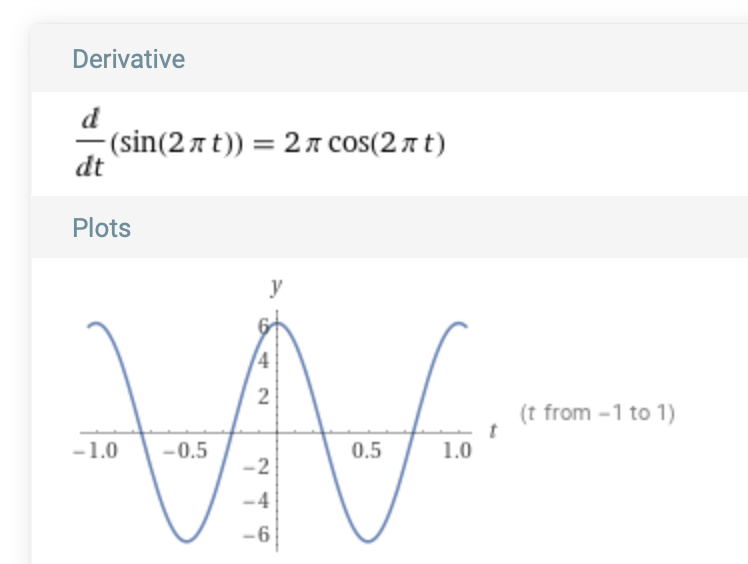
Apply the Fundamental Theorem of Calculus:

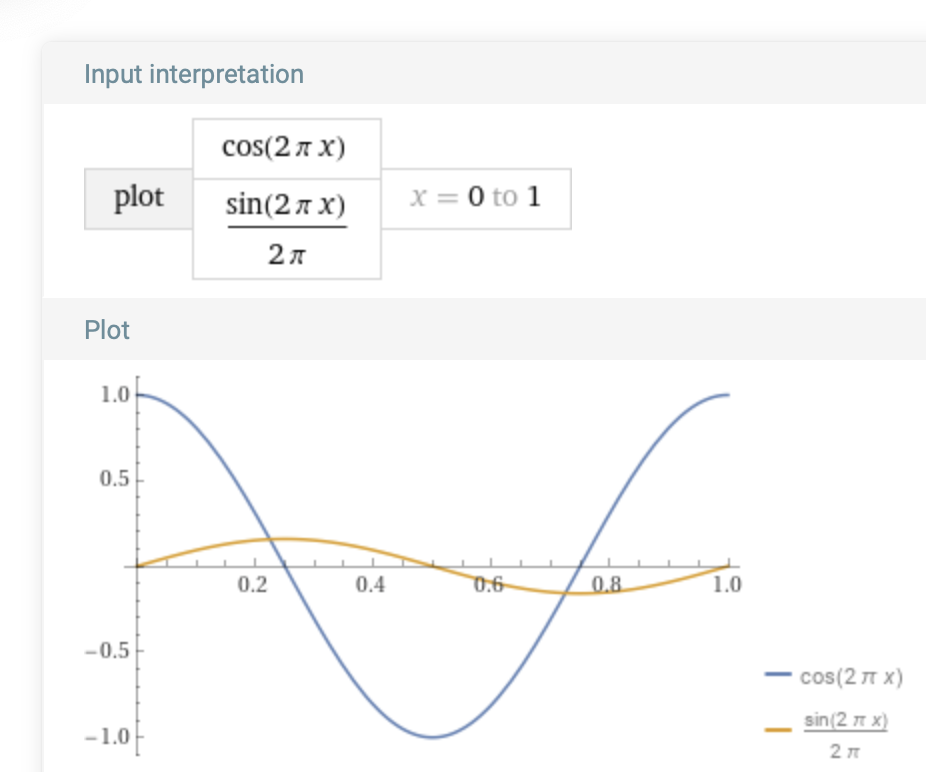
Plot both the integrand cos(2πt) and integral ∫ cos(2πt) together over the unit interval [0,1], their common period:
Alternatively numerical integration of cos(2πt) with vDSP_vsimpsD is used to generate the virtually same result in a SwiftUI app, implemented below in Sample Source Code, and displayed in a window:
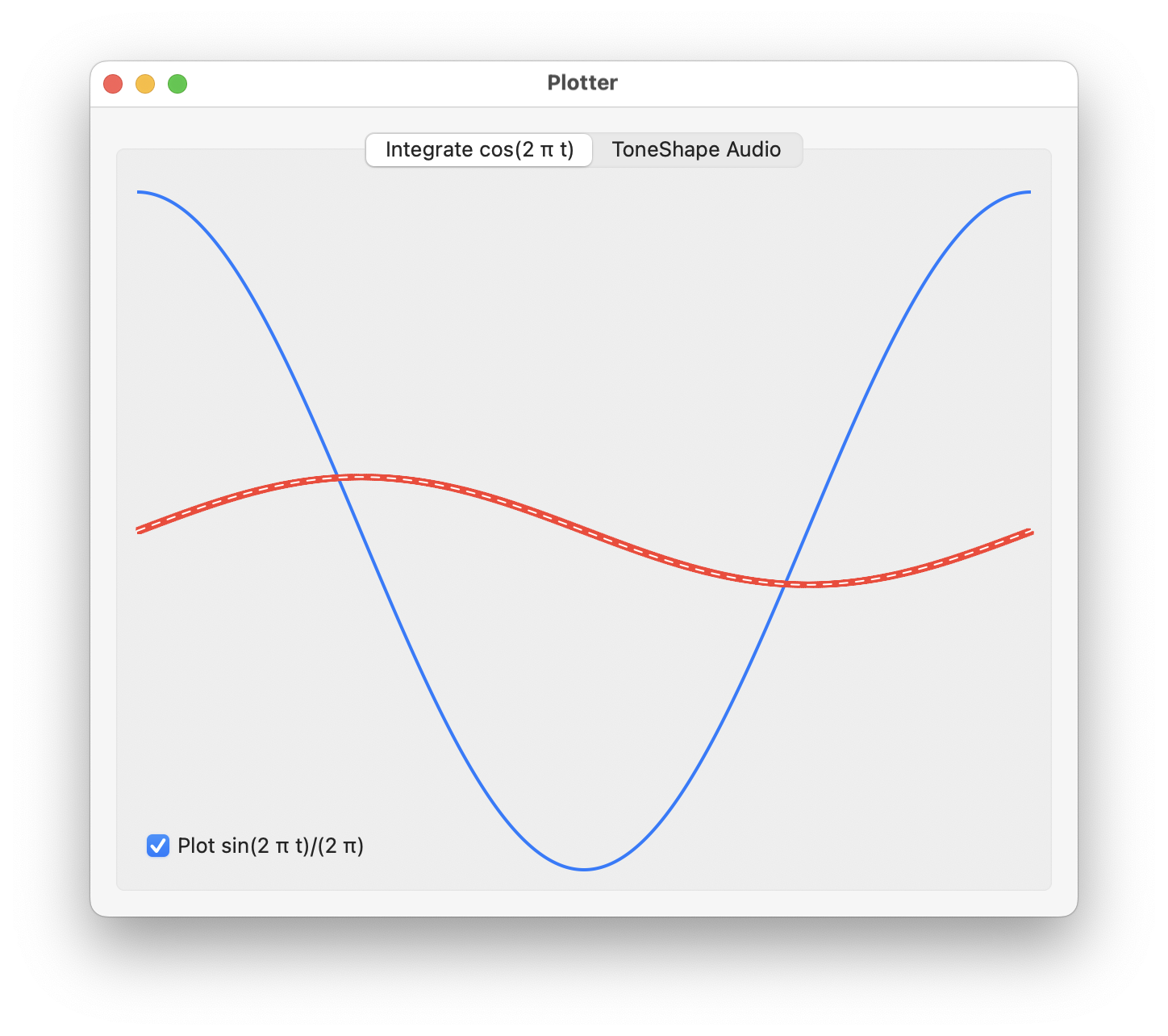
In the initializer of the class IntegrationPlotter, the integrand cos(2πt) of period is 1 is sampled at N points in the interval [0,1] storing the values in integrand_points:
class IntegrationPlotter {
var integrand_points:[CGPoint] = [] // cosine
var integral:[Double] = []
let N:Int
let delta:Double
init() {
N = 500
delta = 1.0/Double(N)
for i in 0...N {
let t = Double(i) * delta
integrand_points.append(CGPoint(x: t, y: cos(2.0 * .pi * t)))
}
let values = integrand_points.map { p in
Double(p.y)
}
integral = integrate(samples: values)
}
An interpolation function is defined for plotting the samples of cos(2πt), which is not the same as plotting cos(2πt) as an actual known function of t:
func interpolate(t: Double, points: [CGPoint]) -> Double {
// Check if t is out of range
if t < points[0].x || t > points[points.count - 1].x {
return 0.0
}
// Find the largest index i such that c[i].x <= t
var i = 0
while i < points.count - 1 && points[i + 1].x <= t {
i += 1
}
// Perform linear interpolation
let x0 = points[i].x
let y0 = points[i].y
if i < points.count - 1 {
let x1 = points[i + 1].x
let y1 = points[i + 1].y
let interpolatedValue = y0 + (y1 - y0) * (t - x0) / (x1 - x0)
return interpolatedValue
} else {
return y0
}
}
This way a function instantaneous_frequency can be defined for any t given the points integrand_points:
func instantaneous_frequency(_ t:CGFloat) -> CGFloat {
return interpolate(t: t, points: integrand_points)
}
The integration is performed using a function integrate which returns an array whose elements are the partial integrals of the integrand cos(2πt) for each point in the grid on which it is sampled:
func integrate(samples:[Double]) -> [Double] {
let sampleCount = samples.count
var step = 1.0 / Double(sampleCount)
var result = [Double](repeating: 0.0, count: sampleCount)
vDSP_vsimpsD(samples, 1, &step, &result, 1, vDSP_Length(sampleCount))
return result
}
This function was applied in the init of Plotter, and the result in integral is then used to define a function sampling_argument to plot it:
func sampling_argument(_ t:CGFloat) -> CGFloat {
let i = Int((t / delta).rounded(.down))
return integral[i]
}
The functions instantaneous_frequency and sampling_argument are passed as arguments to a function that creates SwiftUI Path’s to draw in a View for t in [0,1]:
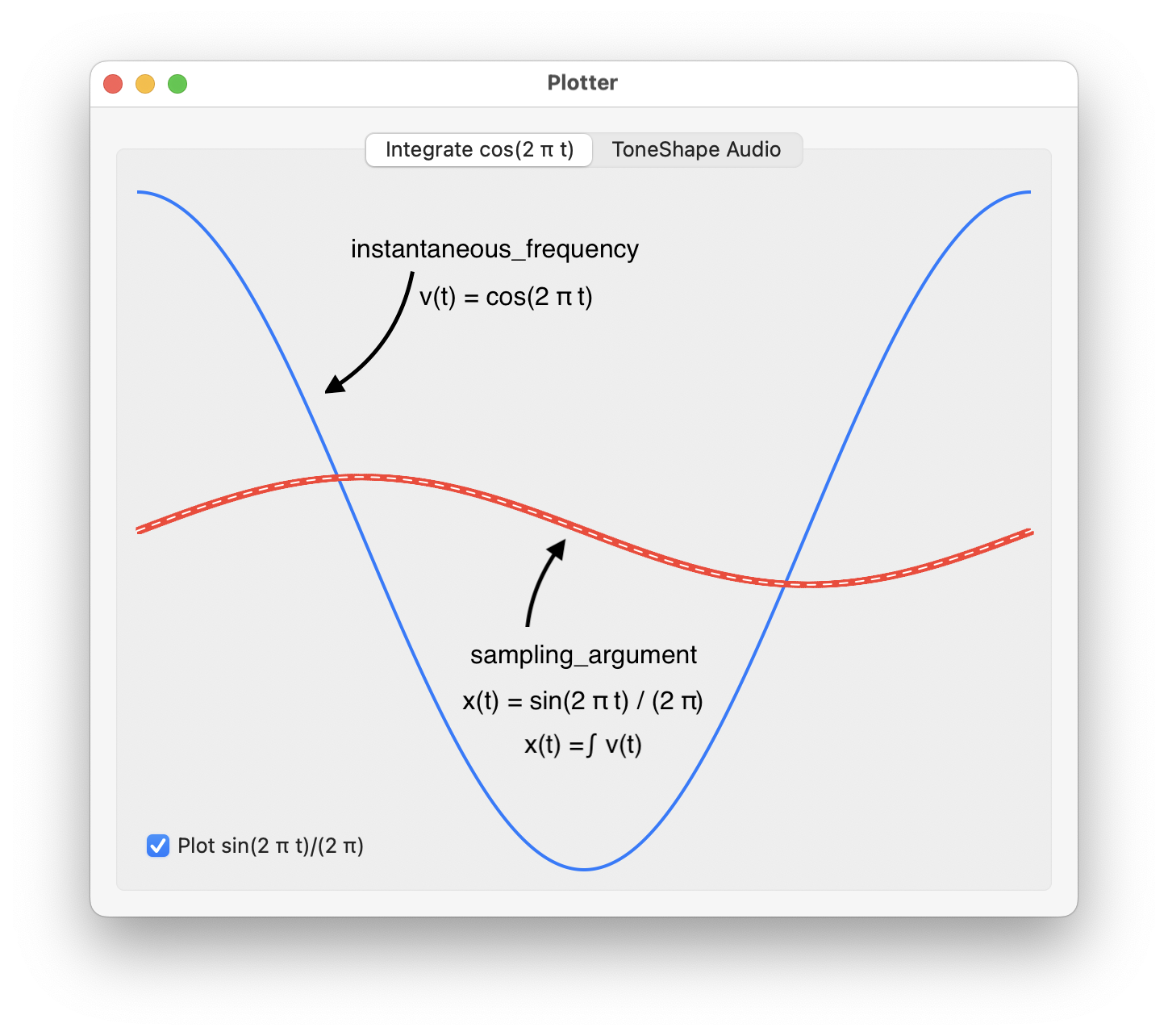
The sampling_argument can then be used for sampling a periodic function to create an audio signal whose frequency at each time is given by the instantaneous_frequency.
To verify the numerical integration the actual integral sin(2 π t) / (2 π), or antiderivative of cos(2 π t), is also plotted as a white dashed path:
func actual_integral(_ t:CGFloat) -> CGFloat {
return sin(2 * .pi * t) / (2 * .pi)
}
Piecewise Integration
The instantaneous frequency values drawn by the user define a function of time, v(t). The function v(t) is numerically integrated with vDSP_vtrapzD to generate a time varying phase argument x(t) of a periodic function s(t):
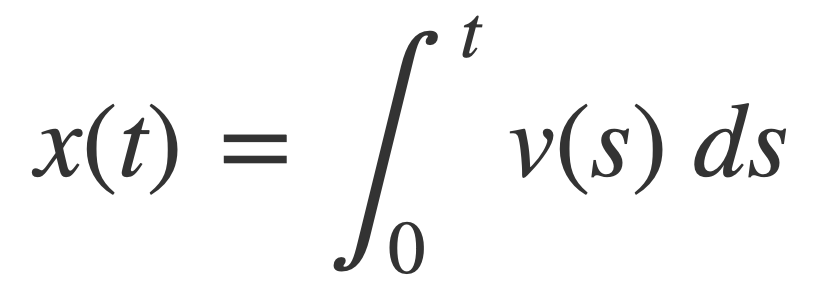
The sampling function s(t) is chosen by the user as one of the Unit Functions, or their Fourier series counterparts. The composition s(x(t)) is sampled at a sufficient rate to produce audio samples of varying frequency for playing or writing to a file.
According to the Nyquist-Shannon sampling theorem audio should be sampled at a rate of 44100 samples per second for high fidelity. At the standard sampling rate of 44100 samples per second, and depending on the desired duration, the memory requirement for an array that holds all audio samples could be very large. Additionally, audio samples are usually packaged into smaller buffers for progressive playing or writing to files. For example the ToneWriter class method saveComponentSamplesToFile saves audio samples to a file by writing a series of CMSampleBuffer, each holding a bufferSize of 8192 samples per request by the AVAssetWriterInput that is attached to an AVAssetWriter. Similarly to play audio with AVAudioEngine the AVAudioSourceNodeRenderBlock typically requests a frameCount of under 1000 samples repeatedly for as long as playing continues.
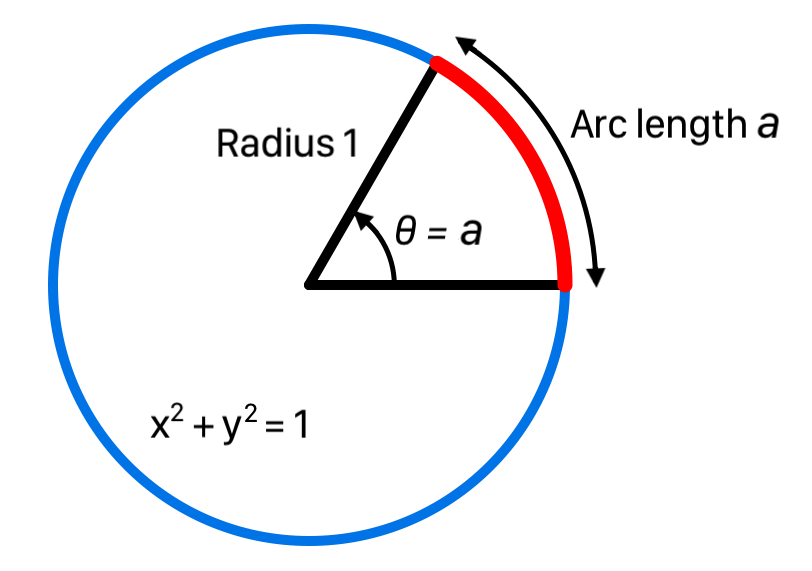
Piecewise integration serves the purpose of generating only enough samples needed per sample buffer request, reducing memory requirements. The integration at any time only requires a subset of the instantaneous frequency values for all samples, sampleIFValues, specified by an index range determined by the current time range of the current audio sample buffer request, and provide by piecewise interpolation. Piecewise integration is based on the additive property of integration, where for any number c in the interval [a, b] and partition [a, c] and [c,b], the integrals add up as follows:
If the integral is interpreted as the area under the integrand’s curve then this property says total area over [a, b] is the sum of the areas over [a, c] and [c,b]. The additive property of integration is used by the PiecewiseIntegrator class to perform the integrations progressively for the range of the current audio sample buffer, providing integration of sampleIFValues as needed.
Each value in sampleIFValues[i] specifies the desired instantaneous frequency at time t = i * stepSize, where stepSize = 1 / sampleRate. To generate the audio sample at this time the sampleIFValues are integrated up to this time. The value of that integral is the argument x(t) of the current sampling function. The following method produces an array of partial integrals for any set of samples:[Double], using either vDSP_vsimpsD or vDSP_vtrapzD. The value of each element of the array returned is the partial integral up to its index, so the last value is the integral of all the samples:
import Accelerate
func integrate(samples:[Double], stepSize:Double, useSimpsons:Bool) -> [Double] {
let sampleCount = samples.count
var step = stepSize
var result = [Double](repeating: 0.0, count: sampleCount)
if useSimpsons {
vDSP_vsimpsD(samples, 1, &step, &result, 1, vDSP_Length(sampleCount))
}
else {
vDSP_vtrapzD(samples, 1, &step, &result, 1, vDSP_Length(sampleCount))
}
return result
}
For example, while playing audio for feedback the AVAudioSourceNodeRenderBlock requests frameCount samples, and a ClosedRange<Int> of indices is formed using the currentIndex property of the AudioEngineManager that keeps track of the first index of the next sample buffer:
let sampleRange = currentIndex...currentIndex+Int(frameCount-1)
The PiecewiseIntegrator obtains the set of instantaneous frequencies for this range with piecewise interpolation and generates a set of partial integrals using integrate. If there was a previous set of partial integrals, then the additive property of integration is applied, and the last value of any previous set of partial integrals is added to each of the current partial integrals.
Numerical integration with vDSP_vtrapzD is chosen because the trapezoid integration algorithm preserves the additivity of numerical integrals implemented here, based on the formula listed in the Swift interface:
Trapezoidal Rule Algorithm
public func vDSP_vtrapzD(_ __A: UnsafePointer<Double>, _ __IA: vDSP_Stride, _ __B: UnsafePointer<Double>, _ __C: UnsafeMutablePointer<Double>, _ __IC: vDSP_Stride, _ __N: vDSP_Length)
/* Maps: The default maps are used.
These compute:
C[0] = 0;
for (n = 1; n < N; ++n)
C[n] = C[n-1] + B[0] * (A[n-1] + A[n])/2;
*/
The computation of each integral C[n] requires only the previous integral C[n-1] and the current and previous sample values A[n-1] and A[n], and B, the ‘step size’ between the samples. It is for this reason the additive property of integration is preserved with this method.
On the other hand, for vDSP_vsimpsD, the Swift interface indicates the Simpson’s rule algorithm:
Simpson’s Rule Algorithm
public func vDSP_vsimpsD(_ __A: UnsafePointer<Double>, _ __IA: vDSP_Stride, _ __B: UnsafePointer<Double>, _ __C: UnsafeMutablePointer<Double>, _ __IC: vDSP_Stride, _ __N: vDSP_Length)
/* Maps: The default maps are used.
These compute:
C[0] = 0;
C[1] = B[0] * (A[0] + A[1])/2;
for (n = 2; n < N; ++n)
C[n] = C[n-2] + B[0] * (A[n-2] + 4*A[n-1] + A[n])/3;
*/
In this case C[n] depends on C[n-2] and A[n-2] in addition to A[n], and requires special setup for the first value C[1]. It is for this reason the additive property of integration is not preserved with this method.
An example will illustrate how piecewise integration with the Trapezoidal rule will be implemented by a procedure for the addition of partial integrals that produces the same result as the full integral. Other examples then illustrate that the Simpson’s rule is not used because the same procedure for the addition of partial integrals may not yield the same result as the full integral.
As it turns out the discrepancy using Simpsons rule may not produce a noticeable effect on the audio generated.
Apply Additivity of Integrals
Piecewise numerical integration is straightforward and illustrated first with the constant function f(x) = 1 for all x. Because the antiderivative of 1 is x + c, for any constant c, by the Fundamental Theorem of Calculus:
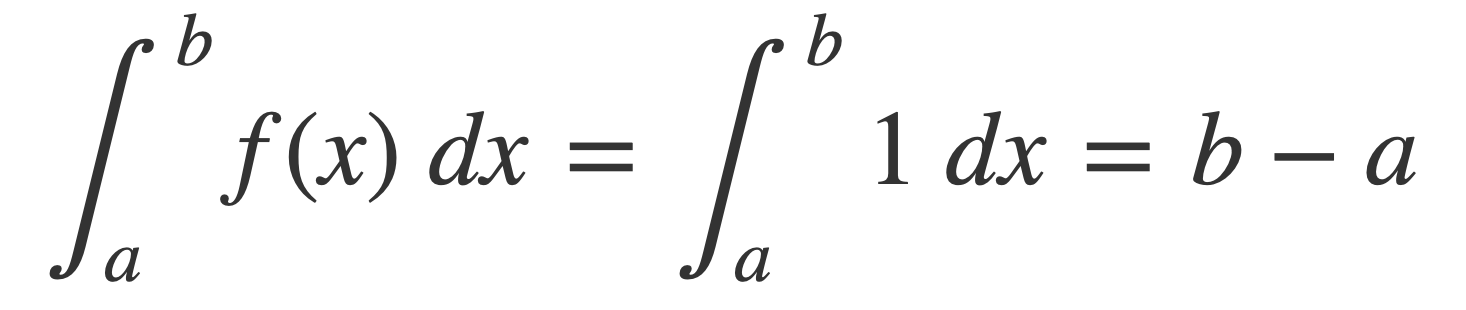
Therefore the integral of 1 over say the interval [0, 2.5] is 2.5 - 0 = 2.5. Now sample the function f(x) = 1 over the interval [0, 2.5] with a sampling step size of 0.25 (so the sample rate is 4) to obtain the array of samples [1,1,1,1, 1,1,1,1, 1,1,1].
Apply the function integrate, in the associated playground:
let sampleRate = 4 // samples per unit interval [0,1)
let delta = 1.0 / Double(sampleRate) // 0.25
print(integrate(samples: [1,1,1,1,1,1,1,1,1,1,1], stepSize: delta, useSimpsons: false))
This prints:
[0.0, 0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5]
The last value 2.5 of the array returned is the exact value of the total integral of 1 over [0,2.5]. The other values in the array are the partial integrals of 1 over intervals [0,0.25], [0,0.5], [0,0.75], etc.
Since functions vary numerical results are not usually exact. For functions that have more variation in values than f(x) = 1 the numerical integral will be an approximation to any exact result, with smaller step sizes generally expected to yield greater accuracy.
Now consider how to evaluate this same integral using piecewise integration on a partition of [0,1] with subintervals, [0.0, 1.5] and [1.5, 2.5], using the additive property of integration. The array of samples is split into two overlapping arrays that cover these intervals, namely:
• [1,1,1,1,1,1,1] for times [0.0, 0.25, 0.5, 0.75, 1.0, 1.25, 1.5]
and
• [1,1,1,1,1] for times [1.5, 1.75, 2.0, 2.25, 2.5]
Note that each array shares the transition time 1.5.
Apply the function integrate, in the associated playground:
print(integrate(samples: [1,1,1,1,1,1,1], stepSize: 0.25, useSimpsons: false))
print(integrate(samples: [1,1,1,1,1] , stepSize: 0.25, useSimpsons: false))
This prints:
[0.0, 0.25, 0.5, 0.75, 1.0, 1.25, 1.5]
[0.0, 0.25, 0.5, 0.75, 1.0]
Apply the the additive property of integrals to adjust the second second array:
The values in the second array of integrals, [0.0, 0.25, 0.5, 0.75, 1.0] are adjusted by adding the total integral of the first array to each element, namely the last element of [0.0, 0.25, 0.5, 0.75, 1.0, 1.25, 1.5], or 1.5. The result in the associated playground is:
var adjusted = vDSP.add(1.5, [0.0, 0.25, 0.5, 0.75, 1.0])
print(adjusted)
This prints:
[1.5, 1.75, 2.0, 2.25, 2.5]
After the adjusted array has the first element removed due to overlap at the transition time, it is concatenated with the first array of integrals to obtain the full array of integrals, in the associated playground:
adjusted.removeFirst()
let full = [0.0, 0.25, 0.5, 0.75, 1.0, 1.25, 1.5] + adjusted
print(full)
This prints the same array of partial integrals when integrating the whole array:
[0.0, 0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5]
Trapezoidal vs. Simpson’s
The Trapezoidal rule algorithm is compared to the Simpson’s rule. In the previous example for the function f(x) = 1 the integration was performed using the trapezoidal rule. Although Simpsons’s rule would have led to the same result, that is not always true.
Apply the same calculations of Apply Additivity of Integrals using an array of samples with more variation using the trapezoidal rule, and then with Simpsons’s rule to exhibit the difference in behavior.
Trapezoidal Rule
In the associated playground calculate the whole array of partial integrals of [4,5,2,8,6,3,1,9,5,3,4,7,8] using the trapezoidal rule with the integrate function:
let sampleRate = 4 // samples per unit interval [0,1)
let delta = 1.0 / Double(sampleRate) // 0.25
print(integrate(samples: [4,5,2,8,6,3,1,9,5,3,4,7,8], stepSize: delta, useSimpsons: false))
This prints:
[0.0, 1.125, 2.0, 3.25, 5.0, 6.125, 6.625, 7.875, 9.625, 10.625, 11.5, 12.875, 14.75]
Consider the overlapping partition [4,5,2,8,6,3,1,9] and [9,5,3,4,7,8], in the associated playground:
let first = integrate(samples: [4,5,2,8,6,3,1,9], stepSize: delta, useSimpsons: false)
let second = integrate(samples: [9,5,3,4,7,8], stepSize: delta, useSimpsons: false)
let lastElement = first[first.count-1]
var adjusted = vDSP.add(lastElement, second)
adjusted.removeFirst()
let full = first + adjusted
print(full)
Run the associated playground and the following is printed:
[0.0, 1.125, 2.0, 3.25, 5.0, 6.125, 6.625, 7.875, 9.625, 10.625, 11.5, 12.875, 14.75]
[0.0, 1.125, 2.0, 3.25, 5.0, 6.125, 6.625, 7.875, 9.625, 10.625, 11.5, 12.875, 14.75]
The same result was obtained using piecewise integration with the Trapezoidal rule algorithm.
Simpson’s Rule
Consider the same procedure for adding integrals with Simpson’s rule, except setting useSimpsons option to true in the integrate function.
In the associated playground calculate the whole array of partial integrals using the Simpson’s rule with the integrate function:
let sampleRate = 4 // samples per unit interval [0,1)
let delta = 1.0 / Double(sampleRate) // 0.25
print(integrate(samples: [4,5,2,8,6,3,1,9,5,3,4,7,8], stepSize: delta, useSimpsons: true))
This prints:
[0.0, 1.125, 2.1666666666666665, 2.875, 5.5, 5.791666666666666, 7.083333333333333, 7.124999999999999, 10.583333333333332, 9.791666666666666, 12.333333333333332, 11.958333333333332, 15.666666666666666]
Consider the overlapping partition [4,5,2,8,6,3,1,9] and [9,5,3,4,7,8], in the associated playground:
let first = integrate(samples: [4,5,2,8,6,3,1,9], stepSize: delta, useSimpsons: true)
let second = integrate(samples: [9,5,3,4,7,8], stepSize: delta, useSimpsons: true)
let lastElement = first[first.count-1]
var adjusted = vDSP.add(lastElement, second)
adjusted.removeFirst()
let full = first + adjusted
print(full)
Run the associated playground and the following is printed:
[0.0, 1.125, 2.1666666666666665, 2.875, 5.5, 5.791666666666666, 7.083333333333333, 7.124999999999999, 10.583333333333332, 9.791666666666666, 12.333333333333332, 11.958333333333332, 15.666666666666666]
[0.0, 1.125, 2.1666666666666665, 2.875, 5.5, 5.791666666666666, 7.083333333333333, 7.124999999999999, 8.875, 9.791666666666666, 10.625, 11.958333333333332, 13.958333333333332]
The same result is not obtained using piecewise integration with the Simpson’s rule.
Larger Arrays
Now, using a function that can generate much larger arrays with random elements, try piecewise integration on arrays whose size is more realistic. Namely for audio sampled at 44100 Hz. The following code is executed in the associated playground:
import Accelerate
func integrate(samples:[Double], stepSize:Double, useSimpsons:Bool) -> [Double] {
let sampleCount = samples.count
var step = stepSize
var result = [Double](repeating: 0.0, count: sampleCount)
if useSimpsons {
vDSP_vsimpsD(samples, 1, &step, &result, 1, vDSP_Length(sampleCount))
}
else {
vDSP_vtrapzD(samples, 1, &step, &result, 1, vDSP_Length(sampleCount))
}
return result
}
func createPartitionRanges(sampleCount: Int, rangeCount: Int) -> [ClosedRange<Int>] {
guard rangeCount > 0 else {
return []
}
var ranges: [ClosedRange<Int>] = []
var start = 0
while start < sampleCount {
let end = min(start + rangeCount, sampleCount) - 1
let range = start...end
ranges.append(range)
start = end + 1
}
return ranges
}
func generateRandomArray(count: Int, inRange range: ClosedRange<Double>) -> [Double] {
return (1...count).map { _ in Double.random(in: range) }
}
func piecewise_integration_random_array(sampleRate: Int = 44100, duration:Double = 1, bufferSize: Int = 512, useSimpsons:Bool) -> Double {
let delta = 1.0 / Double(sampleRate)
let sampleCount = Int(duration * Double(sampleRate))
let v = generateRandomArray(count: sampleCount, inRange: 20.0...22050)
let partitions = createPartitionRanges(sampleCount: v.count, rangeCount: bufferSize)
let integralWhole = integrate(samples: v, stepSize: delta, useSimpsons: useSimpsons)
var combinedIntegral:[Double] = []
var currentPartition = partitions[0]
var partialV = Array(v[currentPartition])
var lastIntegral = integrate(samples: partialV, stepSize: delta, useSimpsons: useSimpsons)
combinedIntegral = combinedIntegral + lastIntegral
if partitions.count > 1 {
for i in 1...partitions.count-1 {
currentPartition = partitions[i]
partialV = [partialV.last!] + Array(v[currentPartition]) // add overlap
let lastIntegralValue = lastIntegral.last!
lastIntegral = integrate(samples: partialV, stepSize: delta, useSimpsons: useSimpsons)
lastIntegral.removeFirst()
lastIntegral = vDSP.add(lastIntegralValue, lastIntegral)
combinedIntegral = combinedIntegral + lastIntegral
}
}
var difference = vDSP.subtract(combinedIntegral, integralWhole)
difference = vDSP.absolute(difference)
let maxAbsDiff = vDSP.maximum(difference)
print("max absolute difference = \(maxAbsDiff)")
return maxAbsDiff
}
var maxmaxAbsDiff = 0.0
var minmaxAbsDiff = Double.greatestFiniteMagnitude
for _ in 0...9 {
let useSimpsons = false
let maxAbsDiff = piecewise_integration_random_array(useSimpsons: useSimpsons)
if maxAbsDiff > maxmaxAbsDiff {
maxmaxAbsDiff = maxAbsDiff
}
if maxAbsDiff < minmaxAbsDiff {
minmaxAbsDiff = maxAbsDiff
}
}
print("maxmaxAbsDiff = \(maxmaxAbsDiff)")
print("minmaxAbsDiff = \(minmaxAbsDiff)")
In a loop, this code integrates 44100 values, randomly selected from 20.0...22050, as a whole and with the piecewise integration procedure of the previous examples. The maximum absolute value of the difference of the corresponding elements of the results for all iterations is printed. For the Simpsons rule, this typically prints results that exhibit large differences, such as:
maxmaxAbsDiff = 26.856620683829533
minmaxAbsDiff = 10.90965610277999
For the trapezoidal rule, this typically prints results that exhibit small differences, such as:
maxmaxAbsDiff = 1.8735590856522322e-10
minmaxAbsDiff = 4.9112713895738125e-11
As it turns out the larger discrepancies using Simpsons rule may not produce a noticeable effect on the audio generated.
Generate Audio
The method of integration discussed in Piecewise Integration is used to generate a WAV audio file. The code snippets are taken from the full Sample Source Code that comprise a complete SwiftUI app used to create the screenshots and the audio file.
The userIFCurve is defined using two arrays to distinguish the abscissa (x) and ordinate (y) of each point of the curve:
let N:Double = 6
let DF:Double = N/6
let x:[Double] = [0 * DF, 1 * DF, 2 * DF, 3 * DF, 4 * DF, 5 * DF, 6 * DF]
let y:[Double] = [30,440,50,440,50,440,50]
let userIFCurve:[CGPoint] = [CGPoint(x: x[0], y: y[0]), CGPoint(x: x[1], y: y[1]), CGPoint(x: x[2], y: y[2]), CGPoint(x: x[3], y: y[3]), CGPoint(x: x[4], y: y[4]), CGPoint(x: x[5], y: y[5]), CGPoint(x: x[6], y: y[6])]
Integration of the instantaneous frequency defined by the userIFCurve is performed by the PiecewiseIntegrator.swift class. However, as an example the piecewise_integrator is used to calculate the whole array of partial integrals for all samples with a while loop:
let sampleCount = Int(duration * Double(sampleRate))
let stepSize = 1.0 / Double(sampleRate)
let piecewise_integrator = PiecewiseIntegrator(userIFCurve: userIFCurve, sampleCount: sampleCount, rangeCount: bufferSize, delta: stepSize)
while let piecewiseIntegral = piecewise_integrator.nextIntegral() {
integral = integral + piecewiseIntegral
}
In the actual implementation the PiecewiseIntegrator.swift is used as intended, computing the partial integrals as audio sample buffers are requested, specified by the current sampleRange for either live audio, as discussed in Tone Generation or when writing files with ToneWriter.
A similar calculation is performed in the AudioPlotter.swift where the integral, x(t), is used as the argument of the signal s(t) = sin(2 * .pi * t), to sample s(x(t)) = sin(2 * .pi * x(t)):
func audio_samples(_ t:CGFloat) -> CGFloat? {
if indexForTime(t) >= 0 && indexForTime(t) < integral.count {
return 10 * sin(2 * .pi * integral[indexForTime(t)])
}
return nil
}
Then audio_samples (scaled by 10 for contrast) are plotted alongside the instantaneous frequency values [30,440,50,440,50,440,50]. The instantaneous frequency values are interpolated (stretched) over the same duration as the integration:
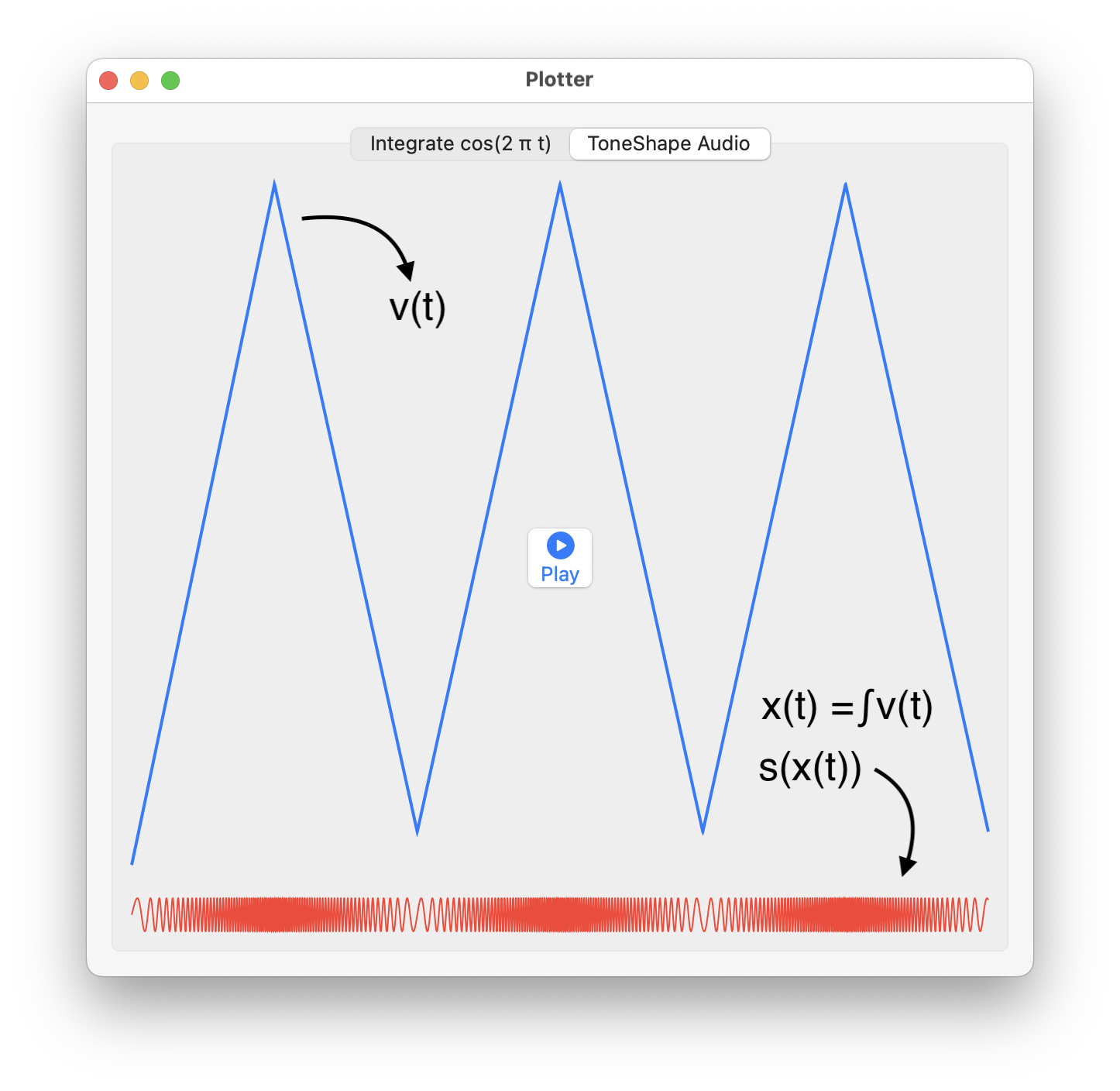
The partial integral values, integral, are similarly used by audioSamplesForRange in the ToneWriter to create audio samples as Int16 values to create audio sample buffers in sampleBufferForSamples:
func audioSamplesForRange(sampleRate:Int, sampleRange:ClosedRange<Int>) -> [Int16] {
var samples:[Int16] = []
let delta_t:Double = 1.0 / Double(sampleRate)
for i in sampleRange.lowerBound...sampleRange.upperBound {
let t = Double(i) * delta_t
let x = integral[i]
var value = sin(2 * .pi * x) * Double(Int16.max)
if let scale = scale {
value = scale(t) * value
}
let valueInt16 = Int16(max(min(value, Double(Int16.max)), Double(Int16.min)))
samples.append(valueInt16)
}
return samples
}
The audio samples buffers are written to a file using AVAssetWriter to generate this audio file, that can be listened to here:
Sample Source Code
The sample audio file in the previous section is generated by the code here, specifically the function GenerateToneShapeAudio in ToneWriter.swift.
The self-contained files can be copied and added to a multi-platform SwiftUI Xcode project and run on macOS and iOS, or download the ToneShaperPreview project.
GeneratePath.swift
import SwiftUI
func GeneratePath(a:CGFloat, b:CGFloat, N:Int, frameSize:CGSize, inset:CGFloat = 10.0, graphs: [(_ x:CGFloat) -> CGFloat?]) -> [Path] {
guard frameSize.width > 0, frameSize.height > 0 else {
return Array(repeating: Path(), count: graphs.count)
}
var plots:[[CGPoint]] = []
var minimum_y:CGFloat = 0
var maximum_y:CGFloat = 0
var minimum_x:CGFloat = 0
var maximum_x:CGFloat = 0
for graph in graphs {
var plot:[CGPoint] = []
for i in 0...N {
let x = a + (CGFloat(i) * ((b - a) / CGFloat(N)))
if let y = graph(x) {
if y < minimum_y {
minimum_y = y
}
if y > maximum_y {
maximum_y = y
}
if x < minimum_x {
minimum_x = x
}
if x > maximum_x {
maximum_x = x
}
plot.append(CGPoint(x: x, y: y))
}
}
plots.append(plot)
}
let frameRect = CGRect(x: 0, y: 0, width: frameSize.width, height: frameSize.height)
let plotRect = frameRect.insetBy(dx: inset, dy: inset)
let x0 = plotRect.origin.x
let y0 = plotRect.origin.y
let W = plotRect.width
let H = plotRect.height
func tx(_ x:CGFloat) -> CGFloat {
if maximum_x == minimum_x {
return x0 + W
}
return (x0 + W * ((x - minimum_x) / (maximum_x - minimum_x)))
}
func ty(_ y:CGFloat) -> CGFloat {
if maximum_y == minimum_y {
return frameSize.height - (y0 + H)
}
return frameSize.height - (y0 + H * ((y - minimum_y) / (maximum_y - minimum_y))) // subtract from frameSize.height to flip coordinates
}
// map points into plotRect using linear interpolation
for i in 0...plots.count-1 {
for j in 0...plots[i].count-1 {
let x = plots[i][j].x
let y = plots[i][j].y
plots[i][j].x = tx(x)
plots[i][j].y = ty(y)
}
}
// create the paths
var paths:[Path] = []
for i in 0...plots.count-1 {
let path = Path { path in
let x = plots[i][0].x
let y = plots[i][0].y
path.move(to: CGPoint(x: x, y: y))
for j in 1...plots[i].count-1 {
let x = plots[i][j].x
let y = plots[i][j].y
path.addLine(to: CGPoint(x: x, y: y))
}
}
paths.append(path)
}
return paths
}
PiecewiseIntegrator.swift
import Accelerate
class PiecewiseIntegrator {
var userIFCurve:[CGPoint]
var sampleCount: Int
var rangeCount: Int
var delta:Double
var useSimpsons: Bool
var partitions:[ClosedRange<Int>]
var scale:Double
let userIFValues:[Double]
var currentPartition:ClosedRange<Int>
var partialV:[Double]
var lastIntegral:[Double]
var currentIndex = -1
init(userIFCurve:[CGPoint], sampleCount: Int, rangeCount: Int, delta:Double, useSimpsons: Bool) {
self.userIFCurve = userIFCurve
self.sampleCount = sampleCount
self.rangeCount = rangeCount
self.delta = delta
self.useSimpsons = useSimpsons
self.partitions = PiecewiseIntegrator.createPartitionRanges(sampleCount: sampleCount, rangeCount: rangeCount)
self.scale = PiecewiseIntegrator.scale(sampleCount: sampleCount, userIFCurve: userIFCurve)
self.userIFValues = PiecewiseIntegrator.userIFValues_by_interpolateUserIFCurve(userIFCurve: userIFCurve)
self.currentPartition = partitions[0]
self.partialV = PiecewiseIntegrator.sampleIFValuesForRange(scale: scale, sampleRange: currentPartition, userIFValues: userIFValues) // overlap
self.lastIntegral = PiecewiseIntegrator.integrate(samples: partialV, stepSize: delta, useSimpsons: useSimpsons)
print(self.partitions)
}
class func integrate(samples:[Double], stepSize:Double, useSimpsons:Bool) -> [Double] {
let sampleCount = samples.count
var step = stepSize
var result = [Double](repeating: 0.0, count: sampleCount)
if useSimpsons {
vDSP_vsimpsD(samples, 1, &step, &result, 1, vDSP_Length(sampleCount))
}
else {
vDSP_vtrapzD(samples, 1, &step, &result, 1, vDSP_Length(sampleCount))
}
return result
}
class func scale(sampleCount:Int, userIFCurve:[CGPoint]) -> Double {
Double(sampleCount-1) / userIFCurve.last!.x
}
class func createPartitionRanges(sampleCount: Int, rangeCount: Int) -> [ClosedRange<Int>] {
guard rangeCount > 0 else {
return []
}
var ranges: [ClosedRange<Int>] = []
var start = 0
while start < sampleCount {
let end = min(start + rangeCount, sampleCount) - 1
let range = start...end
ranges.append(range)
start = end + 1
}
return ranges
}
class func userIFValues_by_interpolateUserIFCurve(userIFCurve:[CGPoint]) -> [Double] {
let indices = userIFCurve.map { Double($0.x) }
let values = userIFCurve.map { Double($0.y) }
return vDSP.linearInterpolate(values: values, atIndices: indices)
}
class func sampleIFValuesForRange(scale:Double, sampleRange:ClosedRange<Int>, userIFValues:[Double]) -> [Double] {
// scale sample range into user range
let ta = Double(sampleRange.lowerBound) / scale
let tb = Double(sampleRange.upperBound) / scale
var valuesToInterpolate:[Double] = []
var sampleIndices:[Double] = []
func appendInterploatedValue(_ t:Double) {
let delta = (t - t.rounded(.down))
let index = Int(t.rounded(.down))
if delta == 0 || (index+1 > userIFValues.count-1) { // index+1 may be out of bounds when delta = 0, or very nearly 0
valuesToInterpolate.append(userIFValues[index])
}
else {
let interpolated = userIFValues[index] * (1 - delta) + userIFValues[index+1] * delta
valuesToInterpolate.append(interpolated)
}
}
if ta == tb {
appendInterploatedValue(ta)
sampleIndices.append(Double(sampleRange.lowerBound))
}
else {
// start
appendInterploatedValue(ta)
sampleIndices.append(Double(sampleRange.lowerBound))
// middle, if any
var lowerBound = Int(ta.rounded(.up))
if lowerBound == Int(ta.rounded(.down)) {
lowerBound += 1
}
var upperBound = Int(tb.rounded(.down))
if upperBound == Int(tb.rounded(.up)) {
upperBound -= 1
}
if lowerBound <= upperBound {
valuesToInterpolate.append(contentsOf: Array(userIFValues[lowerBound...upperBound]))
sampleIndices.append(contentsOf: (lowerBound...upperBound).map { Double($0) * scale })
}
// end
appendInterploatedValue(tb)
sampleIndices.append(Double(sampleRange.upperBound))
}
sampleIndices = sampleIndices.map { $0 - sampleIndices[0]}
return vDSP.linearInterpolate(values: valuesToInterpolate, atIndices: sampleIndices)
}
func nextIntegral() -> [Double]? {
if currentIndex == self.partitions.count-1 {
return nil
}
else {
currentIndex += 1
if currentIndex == 0 {
return self.lastIntegral
}
else {
currentPartition = partitions[currentIndex]
partialV = [partialV.last!] + PiecewiseIntegrator.sampleIFValuesForRange(scale: scale, sampleRange: currentPartition, userIFValues: userIFValues) // overlap
let lastIntegralValue = lastIntegral.last!
lastIntegral = PiecewiseIntegrator.integrate(samples: partialV, stepSize: delta, useSimpsons: useSimpsons)
lastIntegral.removeFirst()
lastIntegral = vDSP.add(lastIntegralValue, lastIntegral)
return self.lastIntegral
}
}
}
}
ToneWriter.swift
import SwiftUI
import AVFoundation
let kUseSimpsons = false
class ToneWriter {
var useSimpsons: Bool
let kAudioWriterExpectsMediaDataInRealTime = false
let kToneGeneratorQueue = "com.limit-point.tone-generator-queue"
var scale: ((Double)->Double)? // scale factor range in [0,1]
var integral:[Double] = []
init(useSimpsons: Bool) {
self.useSimpsons = useSimpsons
}
deinit {
print("ToneWriter deinit")
}
func audioSamplesForRange(sampleRate:Int, sampleRange:ClosedRange<Int>) -> [Int16] {
var samples:[Int16] = []
let delta_t:Double = 1.0 / Double(sampleRate)
for i in sampleRange.lowerBound...sampleRange.upperBound {
let t = Double(i) * delta_t
let x = integral[i]
var value = sin(2 * .pi * x) * Double(Int16.max)
if let scale = scale {
value = scale(t) * value
}
let valueInt16 = Int16(max(min(value, Double(Int16.max)), Double(Int16.min)))
samples.append(valueInt16)
}
return samples
}
func rangeForIndex(bufferIndex:Int, bufferSize:Int, samplesRemaining:Int?) -> ClosedRange<Int> {
let start = bufferIndex * bufferSize
if let samplesRemaining = samplesRemaining {
return start...(start + samplesRemaining - 1)
}
return start...(start + bufferSize - 1)
}
func sampleBufferForSamples(audioSamples:[Int16], bufferIndex:Int, sampleRate:Int, bufferSize:Int) -> CMSampleBuffer? {
var sampleBuffer:CMSampleBuffer?
let bytesInt16 = MemoryLayout<Int16>.stride
let dataSize = audioSamples.count * bytesInt16
var samplesBlock:CMBlockBuffer?
let memoryBlock:UnsafeMutableRawPointer = UnsafeMutableRawPointer.allocate(
byteCount: dataSize,
alignment: MemoryLayout<Int16>.alignment)
let _ = audioSamples.withUnsafeBufferPointer { buffer in
memoryBlock.initializeMemory(as: Int16.self, from: buffer.baseAddress!, count: buffer.count)
}
if CMBlockBufferCreateWithMemoryBlock(
allocator: kCFAllocatorDefault,
memoryBlock: memoryBlock,
blockLength: dataSize,
blockAllocator: nil,
customBlockSource: nil,
offsetToData: 0,
dataLength: dataSize,
flags: 0,
blockBufferOut:&samplesBlock
) == kCMBlockBufferNoErr, let samplesBlock = samplesBlock {
var asbd = AudioStreamBasicDescription()
asbd.mSampleRate = Float64(sampleRate)
asbd.mFormatID = kAudioFormatLinearPCM
asbd.mFormatFlags = kAudioFormatFlagIsSignedInteger | kAudioFormatFlagIsPacked
asbd.mBitsPerChannel = 16
asbd.mChannelsPerFrame = 1
asbd.mFramesPerPacket = 1
asbd.mBytesPerFrame = 2
asbd.mBytesPerPacket = 2
var formatDesc: CMAudioFormatDescription?
let sampleDuration = CMTimeMakeWithSeconds((1.0 / Float64(sampleRate)), preferredTimescale: Int32.max)
if CMAudioFormatDescriptionCreate(allocator: nil, asbd: &asbd, layoutSize: 0, layout: nil, magicCookieSize: 0, magicCookie: nil, extensions: nil, formatDescriptionOut: &formatDesc) == noErr, let formatDesc = formatDesc {
let sampleTime = CMTimeMultiply(sampleDuration, multiplier: Int32(bufferIndex * bufferSize))
let timingInfo = CMSampleTimingInfo(duration: sampleDuration, presentationTimeStamp: sampleTime, decodeTimeStamp: .invalid)
if CMSampleBufferCreate(allocator: kCFAllocatorDefault, dataBuffer: samplesBlock, dataReady: true, makeDataReadyCallback: nil, refcon: nil, formatDescription: formatDesc, sampleCount: audioSamples.count, sampleTimingEntryCount: 1, sampleTimingArray: [timingInfo], sampleSizeEntryCount: 0, sampleSizeArray: nil, sampleBufferOut: &sampleBuffer) == noErr, let sampleBuffer = sampleBuffer {
guard sampleBuffer.isValid, sampleBuffer.numSamples == audioSamples.count else {
return nil
}
}
}
}
return sampleBuffer
}
func sampleBufferForComponent(sampleRate:Int, bufferSize: Int, bufferIndex:Int, samplesRemaining:Int?) -> CMSampleBuffer? {
let audioSamples = audioSamplesForRange(sampleRate: sampleRate, sampleRange: rangeForIndex(bufferIndex:bufferIndex, bufferSize: bufferSize, samplesRemaining: samplesRemaining))
return sampleBufferForSamples(audioSamples: audioSamples, bufferIndex: bufferIndex, sampleRate: sampleRate, bufferSize: bufferSize)
}
func saveComponentSamplesToFile(userIFCurve:[CGPoint], duration:Double = 3, sampleRate:Int = 44100, bufferSize:Int = 8192, destinationURL:URL, completion: @escaping (URL?, String?) -> ()) {
let sampleCount = Int(duration * Double(sampleRate))
let stepSize = 1.0 / Double(sampleRate)
let piecewise_integrator = PiecewiseIntegrator(userIFCurve: userIFCurve, sampleCount: sampleCount, rangeCount: bufferSize, delta: stepSize, useSimpsons: useSimpsons)
while let piecewiseIntegral = piecewise_integrator.nextIntegral() {
integral = integral + piecewiseIntegral
}
var nbrSampleBuffers = Int(duration * Double(sampleRate)) / bufferSize
let samplesRemaining = Int(duration * Double(sampleRate)) % bufferSize
if samplesRemaining > 0 {
nbrSampleBuffers += 1
}
print(nbrSampleBuffers)
print(piecewise_integrator.partitions.count)
print("samplesRemaining = \(samplesRemaining)")
guard let sampleBuffer = sampleBufferForComponent(sampleRate: sampleRate, bufferSize: bufferSize, bufferIndex: 0, samplesRemaining: nil) else {
completion(nil, "Invalid first sample buffer.")
return
}
var actualDestinationURL = destinationURL
if actualDestinationURL.pathExtension != "wav" {
actualDestinationURL.deletePathExtension()
actualDestinationURL.appendPathExtension("wav")
}
try? FileManager.default.removeItem(at: actualDestinationURL)
guard let assetWriter = try? AVAssetWriter(outputURL: actualDestinationURL, fileType: AVFileType.wav) else {
completion(nil, "Can't create asset writer.")
return
}
let sourceFormat = CMSampleBufferGetFormatDescription(sampleBuffer)
let audioCompressionSettings = [AVFormatIDKey: kAudioFormatLinearPCM] as [String : Any]
if assetWriter.canApply(outputSettings: audioCompressionSettings, forMediaType: AVMediaType.audio) == false {
completion(nil, "Can't apply compression settings to asset writer.")
return
}
let audioWriterInput = AVAssetWriterInput(mediaType: AVMediaType.audio, outputSettings:audioCompressionSettings, sourceFormatHint: sourceFormat)
audioWriterInput.expectsMediaDataInRealTime = kAudioWriterExpectsMediaDataInRealTime
if assetWriter.canAdd(audioWriterInput) {
assetWriter.add(audioWriterInput)
} else {
completion(nil, "Can't add audio input to asset writer.")
return
}
let serialQueue: DispatchQueue = DispatchQueue(label: kToneGeneratorQueue)
assetWriter.startWriting()
assetWriter.startSession(atSourceTime: CMTime.zero)
func finishWriting() {
assetWriter.finishWriting {
switch assetWriter.status {
case .failed:
var errorMessage = ""
if let error = assetWriter.error {
let nserr = error as NSError
let description = nserr.localizedDescription
errorMessage = description
if let failureReason = nserr.localizedFailureReason {
print("error = \(failureReason)")
errorMessage += ("Reason " + failureReason)
}
}
completion(nil, errorMessage)
print("saveComponentsSamplesToFile errorMessage = \(errorMessage)")
return
case .completed:
print("saveComponentsSamplesToFile completed : \(actualDestinationURL)")
completion(actualDestinationURL, nil)
return
default:
print("saveComponentsSamplesToFile other failure?")
completion(nil, nil)
return
}
}
}
var bufferIndex = 0
audioWriterInput.requestMediaDataWhenReady(on: serialQueue) { [weak self] in
while audioWriterInput.isReadyForMoreMediaData, bufferIndex < nbrSampleBuffers {
var currentSampleBuffer:CMSampleBuffer?
if samplesRemaining > 0 {
if bufferIndex < nbrSampleBuffers-1 {
currentSampleBuffer = self?.sampleBufferForComponent(sampleRate: sampleRate, bufferSize: bufferSize, bufferIndex: bufferIndex, samplesRemaining: nil)
}
else {
currentSampleBuffer = self?.sampleBufferForComponent(sampleRate: sampleRate, bufferSize: bufferSize, bufferIndex: bufferIndex, samplesRemaining: samplesRemaining)
}
}
else {
currentSampleBuffer = self?.sampleBufferForComponent(sampleRate: sampleRate, bufferSize: bufferSize, bufferIndex: bufferIndex, samplesRemaining: nil)
}
if let currentSampleBuffer = currentSampleBuffer {
audioWriterInput.append(currentSampleBuffer)
}
bufferIndex += 1
if bufferIndex == nbrSampleBuffers {
audioWriterInput.markAsFinished()
finishWriting()
}
}
}
}
}
var toneWriter = ToneWriter(useSimpsons: kUseSimpsons)
func GenerateToneShapeAudio() {
let duration:Double = 1.0
let scale:((Double)->Double) = {t in 1 - (t / duration)}
// equally spaced
let N:Double = 6
let DF:Double = N/6
let x:[Double] = [0 * DF, 1 * DF, 2 * DF, 3 * DF, 4 * DF, 5 * DF, 6 * DF]
let y:[Double] = [30,440,50,440,50,440,50]
let userIFCurve:[CGPoint] = [CGPoint(x: x[0], y: y[0]), CGPoint(x: x[1], y: y[1]), CGPoint(x: x[2], y: y[2]), CGPoint(x: x[3], y: y[3]), CGPoint(x: x[4], y: y[4]), CGPoint(x: x[5], y: y[5]), CGPoint(x: x[6], y: y[6])]
var audioFileURL:URL
do {
let documentsDirectory = try FileManager.default.url(for: .documentDirectory, in: .userDomainMask, appropriateFor: nil, create: false)
audioFileURL = documentsDirectory.appendingPathComponent("ToneShape.wav")
} catch {
return
}
toneWriter.scale = scale
toneWriter.saveComponentSamplesToFile(userIFCurve: userIFCurve, duration: duration, destinationURL: audioFileURL) { resultURL, message in
if let resultURL = resultURL {
let asset = AVAsset(url: resultURL)
Task {
do {
let duration = try await asset.load(.duration)
print("ToneWriter : audio duration = \(duration.seconds)")
}
catch {
}
}
}
else {
print("An error occurred : \(message ?? "No error message available.")")
}
}
}
AudioPlotter.swift
import Foundation
class AudioPlotter {
let sampleCount = 44100
let bufferSize = 526
var allSampleIFValues:[Double] = []
var integral:[Double] = []
var useSimpsons: Bool
init(useSimpsons: Bool) {
self.useSimpsons = useSimpsons
// equally spaced
let N:Double = 6
let DF:Double = N/6
let x:[Double] = [0 * DF, 1 * DF, 2 * DF, 3 * DF, 4 * DF, 5 * DF, 6 * DF]
let y:[Double] = [30,440,50,440,50,440,50]
let userIFCurve:[CGPoint] = [CGPoint(x: x[0], y: y[0]), CGPoint(x: x[1], y: y[1]), CGPoint(x: x[2], y: y[2]), CGPoint(x: x[3], y: y[3]), CGPoint(x: x[4], y: y[4]), CGPoint(x: x[5], y: y[5]), CGPoint(x: x[6], y: y[6])]
// scale up
let scale = PiecewiseIntegrator.scale(sampleCount: sampleCount, userIFCurve: userIFCurve)
let userIFValues = PiecewiseIntegrator.userIFValues_by_interpolateUserIFCurve(userIFCurve: userIFCurve)
let partition = PiecewiseIntegrator.createPartitionRanges(sampleCount: sampleCount, rangeCount: bufferSize)
// compute allSampleIFValues - all samples values by partitioning
for sampleRange in partition {
let sampleIFValuesForRange = PiecewiseIntegrator.sampleIFValuesForRange(scale: scale, sampleRange: sampleRange, userIFValues: userIFValues)
allSampleIFValues.append(contentsOf: sampleIFValuesForRange)
}
let stepSize = 1.0 / Double(sampleCount)
let piecewise_integrator = PiecewiseIntegrator(userIFCurve: userIFCurve, sampleCount: sampleCount, rangeCount: bufferSize, delta: stepSize, useSimpsons: useSimpsons)
while let piecewiseIntegral = piecewise_integrator.nextIntegral() {
integral = integral + piecewiseIntegral
}
}
func indexForTime(_ t:Double) -> Int {
let stepSize = 1/Double(sampleCount)
return Int((t / stepSize).rounded(.down))
}
func instantaneous_frequency(_ t:CGFloat) -> CGFloat? {
if indexForTime(t) >= 0 && indexForTime(t) < allSampleIFValues.count {
return allSampleIFValues[indexForTime(t)]
}
return nil
}
func audio_samples(_ t:CGFloat) -> CGFloat? {
if indexForTime(t) >= 0 && indexForTime(t) < integral.count {
return 10 * sin(2 * .pi * integral[indexForTime(t)])
}
return nil
}
}
IntegrationPlotter.swift
import Accelerate
class IntegrationPlotter {
var integrand_points:[CGPoint] = [] // cosine
var integral:[Double] = []
let N:Int
let delta:Double
init() {
N = 500
delta = 1.0/Double(N)
for i in 0...N {
let t = Double(i) * delta
integrand_points.append(CGPoint(x: t, y: cos(2.0 * .pi * t)))
}
let values = integrand_points.map { p in
Double(p.y)
}
integral = integrate(samples: values)
}
/*
Extend a function by interpolating points
*/
func interpolate(t: Double, points: [CGPoint]) -> Double {
// Check if t is out of range
if t < points[0].x || t > points[points.count - 1].x {
return 0.0
}
// Find the largest index i such that c[i].x <= t
var i = 0
while i < points.count - 1 && points[i + 1].x <= t {
i += 1
}
// Perform linear interpolation
let x0 = points[i].x
let y0 = points[i].y
if i < points.count - 1 {
let x1 = points[i + 1].x
let y1 = points[i + 1].y
let interpolatedValue = y0 + (y1 - y0) * (t - x0) / (x1 - x0)
return interpolatedValue
} else {
return y0
}
}
func integrate(samples:[Double]) -> [Double] {
let sampleCount = samples.count
var step = 1.0 / Double(sampleCount)
var result = [Double](repeating: 0.0, count: sampleCount)
vDSP_vsimpsD(samples, 1, &step, &result, 1, vDSP_Length(sampleCount))
return result
}
// sampled function cos(2 pi x) - red
func instantaneous_frequency(_ t:CGFloat) -> CGFloat {
return interpolate(t: t, points: integrand_points)
}
// numerical integral using sampled function cos(2 pi x) - black
// ∫cos(2 pi x) = sin(2 pi x)/(2 pi)
func sampling_argumemt(_ t:CGFloat) -> CGFloat {
let i = Int((t / delta).rounded(.down))
return integral[i]
}
// actual integral cos(2 pi x) - white, dashed
// ∫cos(2 pi x) = sin(2 pi x)/(2 pi)
func actual_integral(_ t:CGFloat) -> CGFloat {
return sin(2 * .pi * t) / (2 * .pi)
}
}
ContentView.swift
import SwiftUI
import AVFoundation
class AudioPlayerManager: ObservableObject {
var audioPlayer: AVAudioPlayer?
func playAudio(from url: URL) {
do {
audioPlayer = try AVAudioPlayer(contentsOf: url)
audioPlayer?.play()
} catch {
print("Error playing audio: \(error.localizedDescription)")
}
}
}
struct PlayButtonView: View {
@StateObject var audioPlayerManager = AudioPlayerManager()
var body: some View {
Button(action: {
if let audioURL = FileManager.default.urls(for: .documentDirectory, in: .userDomainMask).first?.appendingPathComponent("ToneShape.wav") {
audioPlayerManager.playAudio(from: audioURL)
}
}) {
VStack {
Image(systemName: "play.circle.fill")
.font(.system(size: 18))
.foregroundColor(.blue)
Text("Play")
.foregroundColor(.blue)
}
}
}
}
struct ContentView: View {
@State private var selection = 1
let plotter = IntegrationPlotter()
let audioPlotter = AudioPlotter(useSimpsons: kUseSimpsons)
@State var plotter_paths = [Path(), Path(), Path()]
@State var audio_paths = [Path(), Path()]
@State var plotActualIntegral = true
func updatePlotterPaths(frameSize: CGSize) {
plotter_paths = GeneratePath(a: 0, b: 1, N: 10000, frameSize: frameSize, inset: 10, graphs: [plotter.instantaneous_frequency(_:), plotter.sampling_argumemt(_:), plotter.actual_integral(_:)])
}
func updateAudioPaths(frameSize: CGSize) {
audio_paths = GeneratePath(a: 0, b: 1, N: 30000, frameSize: frameSize, inset: 10, graphs: [audioPlotter.instantaneous_frequency(_:), audioPlotter.audio_samples(_:)])
}
var body: some View {
TabView(selection: $selection) {
// Tab 1 for IntegrationPlotter
GeometryReader { geometry in
ZStack(alignment: .bottomLeading) {
plotter_paths[0]
.stroke(Color.blue, lineWidth: 2)
plotter_paths[1]
.stroke(Color.red, lineWidth: 4)
if plotActualIntegral {
plotter_paths[2]
.stroke(
Color.white,
style: StrokeStyle(
lineWidth: 1,
lineCap: .round,
lineJoin: .round,
dash: [5, 5]
)
)
}
Toggle("Plot sin(2 π t)/(2 π)", isOn: $plotActualIntegral)
.padding()
}
.onAppear {
updatePlotterPaths(frameSize: geometry.size)
}
.onChange(of: geometry.size) { _ in
updatePlotterPaths(frameSize: geometry.size)
}
}
.tabItem {
Label("Integrate cos(2 π t)", systemImage: "sum")
}
.tag(0)
// Tab 2 for AudioPlotter
GeometryReader { geometry in
ZStack {
audio_paths[0]
.stroke(Color.blue, lineWidth: 2)
audio_paths[1]
.stroke(Color.red, lineWidth: 1)
PlayButtonView()
}
.onAppear {
updateAudioPaths(frameSize: geometry.size)
}
.onChange(of: geometry.size) { _ in
updateAudioPaths(frameSize: geometry.size)
}
}
.tabItem {
Label("ToneShape Audio", systemImage: "waveform")
}
.tag(1)
}
.padding()
.onAppear {
DispatchQueue.main.asyncAfter(deadline: .now() + 0.5) {
selection = 0
}
}
}
}
struct ContentView_Previews: PreviewProvider {
static var previews: some View {
ContentView()
}
}
ToneShaperPreviewApp.swift
import SwiftUI
@main
struct ToneShaperPreviewApp: App {
init() {
GenerateToneShapeAudio()
}
var body: some Scene {
WindowGroup {
ContentView()
#if os(macOS)
.onAppear {
if let window = NSApplication.shared.windows.first {
window.title = "Plotter"
}
}
#endif
}
}
}